最小二乘拟合的理解
本文最后更新于:2023年9月14日 晚上
最小二乘拟合的理解
最小二乘法一种数学回归分析的一种方法,通常用于数据拟合,在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域得到广泛应用。起源于十八世纪的大航海探索时期,发展于天文领域和航海领域。法国科学家勒让德于1805年首先提出了最小二乘法,后来在1822年由高斯证明了最小二乘法的优越性,也就是高斯-马尔可夫定理。其中最小二乘其实是日语的翻译,二乘在日语中也就是平方的翻译,中文其实可以称为最小平方法。
参考:
Least Squares Method: What It Means, How to Use It, With Examples (investopedia.com)
数据拟合——非线性最小二乘法 - 知乎 (zhihu.com)
牛顿法 高斯牛顿法 | Cheng Wei's Blog (scm_mos.gitlab.io)
一、基本定义
最小二乘法(又称最小平方法)通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合,其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
若存在一对观测量
为了寻找函数
二、线性最小二乘问题
当拟合函数
例如当给定
将多个观测值带入可获得多个等式方程:
求解参数为
写成向量形式:
则可以理解为1个三维向量由两外2个三维的基向量组成,两个基向量分别是
原理示意如下图所示:
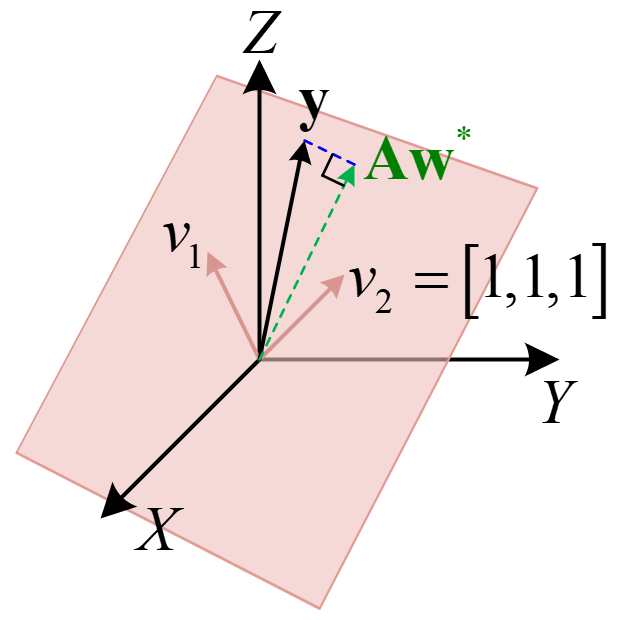
当观测数据变多时,则基向量由原来三维变为高维向量,但其垂直关系不变。仍以三维空间为例,由上式
因为
最终可求解最佳参数
其中:
都是可由观测值获得,由于
若拟合方程为
三、非线性最小二乘问题
当拟合函数
例如当给定
所以为求最佳拟合,则其残差平方和最小,即
求解非线性优化的方法可以主要分为线性搜索法(Line Search)和信赖域法(Trust Region Method)。
其中:高斯牛顿法属于线性搜索法,列文伯格—马夸尔特法属于信赖域法
(1)Line Search
线性搜索核心思想是先确定搜索方向,然后确定步长进行迭代
高斯牛顿法(G-N法):
在任意参数组合
令
至此可以求得迭代步长
其中:
高斯牛顿法计算过程步骤:
相比于牛顿法,高斯牛顿法不用计算 Hessian 矩阵,直接用
(2)Trust Region
信赖域法核心思想则是先确定最大距离,再确定方向。具体为每次迭代都会给出一个半径为
列文伯格-马夸尔特法(L-M法):
Line Search
依赖线性化近似有较高的拟合度,但是有时候线性近似效果较差,导致迭代不稳定;Region
Trust
就是解决了这种问题。高斯牛顿法中采用的近似二阶泰勒展开只在该点附近有较好的近似结果,对
LM法迭代公式:
当
当
对于信赖域
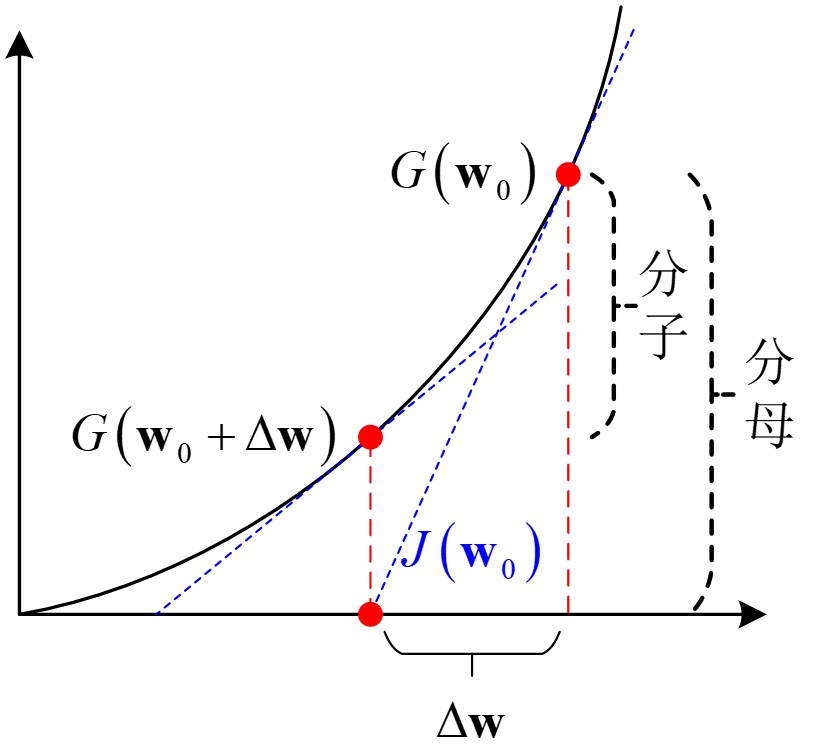
来判断泰勒近似是否够好,
列文伯格-马夸尔特法计算过程步骤:
- 给定初值
- 根据式
- 若
- 若
- 若
- 若
- 判断
- 若不收敛,则更新的参数
- LM法是一种非常高效的迭代算法,能适用于大多数的例子
- 该算法的许多变量决定了迭代的效率和结果的收敛性,而这些参数的理想值往往依目标函数不同而不同
- 因为存在矩阵求逆这一运算,所以对于大型数据求解需要用一些特殊技巧
四、代码示例
太累了,敲不动了。哈哈哈,自己找去吧!
(1)线性最小二乘
(2)非线性最小二乘
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
