滑膜控制SMC（Sliding Mode Control）

本文最后更新于：2023年9月13日 下午

滑模控制

  在控制系统中，滑模控制(SMC)是一种非线性控制方法，它与常规控制的区别在于控制的不连续性。滑模控制是变结构控制的一 个分支。它是一种非线性控制，通过切换函数来实现，根据系统状态偏离滑模面的程度来切换控制器的结构（控制律或控制器参数），从而使系统按照滑模规定的规律运行的控制方法。控制律不是时间的连续函数，它可以根据状态空间中的当前位置从一个连续结构切换到另一个连续结构。因此，滑模控制是一种变结构控制方法。目前已设计有多种控制结构。滑模控制的重要的优点是鲁棒性，当系统处于滑动模态时，对被控对象的模型误差、对象参数的变化以及外部干扰有极佳的不敏感性。滑模控制的缺点：当状态轨迹到达滑动模态面后，难以严格沿着滑动模态面向平衡点滑动，而是在其两侧来回穿越地趋近平衡点，从而产生抖振，这也是滑模控制在实际应用中的主要障碍。

参考：

滑模控制的基本原理

滑模控制学习笔记（一）

滑模控制理论（SMC）概述

滑模控制学习笔记（三）

滑模控制的一些思考-滑模面设计和进阶滑模控制

常系数齐次线性微分方程 - 知乎 (zhihu.com)

一、滑模控制基本概念

  滑模变结构控制的原理，是根据系统所期望的动态特性来设计系统的切换超平面，通过滑动模态控制器使系统状态从超平面之外向切换超平面（也可称为滑模面）收敛靠近。系统一旦到达切换超平面，控制作用将保证系统沿切换超平面到达系统原点，这一沿切换超平面向原点滑动的过程称为滑模控制。由于系统的特性和参数只取决于设计的切换超平面而与外界干扰没有关系，所以滑模变结构控制具有很强的鲁棒性。超平面的设计方法有极点配置，特征向量配置设计法，最优化设计方法等，所设计的切换超平面需满足达到条件，即系统在滑模平面后将保持在该平面的条件。

  对于给定的一个系统，假设它可以用如下形式表示：   则在系统的状态空间存在一个超曲面，它的表达式如下，在下面详述为何使：   则在状态空间中任意一点运动与滑模面（超曲面）的关系可由下图所表示（分三类）：

滑模运动

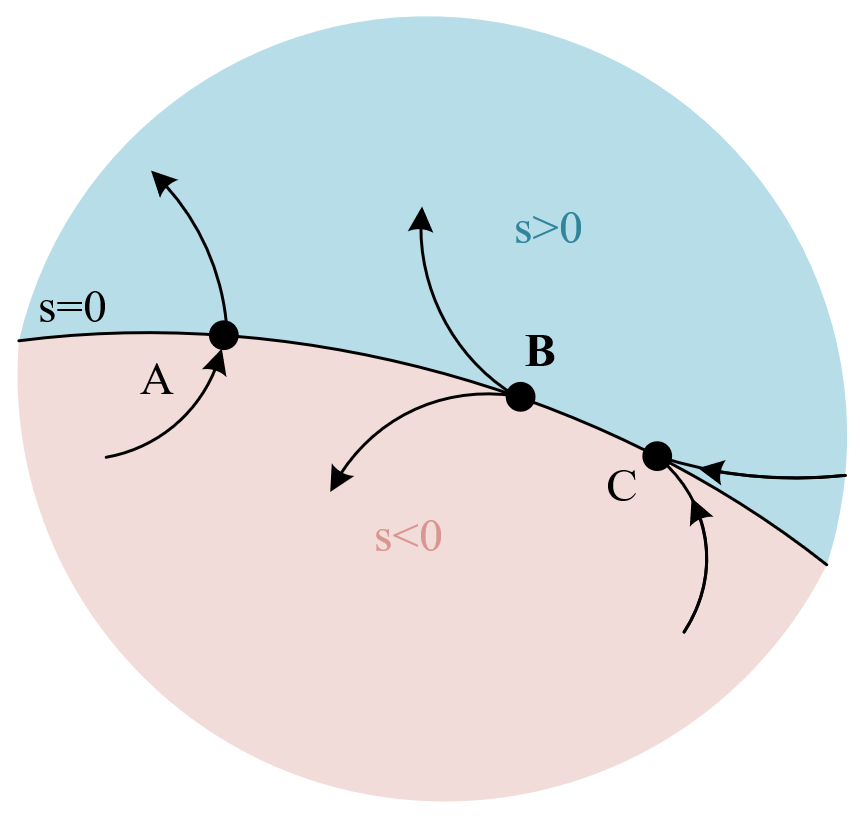
A点：穿越点，它表示系统运动到滑模面的时候并不停留而是直接穿越过去，这时候系统在A点附近时会满足下面的关系： B点：发散点，它表示当系统在滑模面的时候会从其两边离开，这时候系统在B点附近时会满足下面的关系： C点：收敛点，它表示系统运动到滑模面的时候会从停留在滑模面上，这时候系统在C点附近时会满足下面的关系：   在滑模变结构中，穿越点与发散点无多大意义，而收敛点却有特殊的含义，因为如果在切换面上某一区域内所有的点都是收敛点，则一旦运动点趋近于该区域时，就被”吸引“在该区域内运动，即满足滑模到达条件。此时，就称在切换面上所有的运动点都是收敛点的超曲面为“滑模面”。系统在滑模面中的运动就称为“滑模运动”。

二、滑模设计步骤

  在系统控制过程中，控制器根据系统当时状态，以跃变方式有目的地不断变换，迫使系统按预定的“ 滑动模态” 的状态轨迹运动。变结构是通过切换函数实现的，特别要指出的是，通常要求切换面上存在滑动模态区，故变结构控制又常被称为滑动模态控制。设计变结构控制系统基本可分为两步：

(1)确定切换函数s(x)

  即滑模面，设计滑模面，保证系统存在滑模面。它所确定的滑动模态可使系统渐近稳定且有良好的品质滑模面面代表了系统的理想动态特性。

  针对如下线性系统：

  设计滑模面参数：

  为何使，是由于当时，上式可以根据、转化成如下方程：   可知上式方程为常系数齐次线性微分方程，其解与的根有关，当满足Hurwitz稳定判据时，方程的解均存在负实部，则解中的自然指数函数中幂的常系数小于0，则最终会收敛至0，以至于、、…、都会收敛至0。所以滑模面选择此种形式以便于分析，故在滑模控制系统中，参数 应满足Hurwitz稳定判据。

(2)设计滑模控制器

  选择适合的趋近律，设计滑模控制器，使到达条件得到满足，从而使趋近运动 (非滑动模态 )于有限时间到达开关面，并且在趋近的过程中快速、 抖振小。

  举一个例子进行说明，假设系统的状态方程为：   首先设计滑模面，使得滑模面存在，即满足Hurwitz稳定，设计，此时，当时可得，保证了系统存在滑模面。接着为了使系统能够在有限时间内到达滑模面并稳定在其上，采用李雅普诺夫方法进行分析。对于平衡点，如果存在一个连续函数满足以下两个条件，那么系统将在平衡点处稳定：

条件1：

条件2：

  取李雅普诺夫函数为：(显然满足条件1)

  求导得：

  在实际控制器的设计过程中，考虑到不能每次控制输出都要进行一次李雅普诺夫判据，因此通常采用引入趋近律的方式，也就是用一个函数将替换，且均满足滑模到达条件，常见的趋近律有：

  1. 等速趋近律：其中是符号函数
  2. 指数趋近律：
  3. 幂次趋近律：
  4. 一般趋近律：其中，当时，。

  以采用指数趋近律设计控制律为例，则有：（满足条件2）

  采用下述引理，可得，可见，指数收敛至零，收敛速度取决于。指数项能保证当较大时，系统状态能以较大的速度趋近于滑动模态。因此，指数趋近律尤其适合解决具有大阶跃的响应控制问题。

  需要说明的是，指数趋近中，趋近速度从一较大值逐步减小到零，不仅缩短了趋近时间，而且使运动点到达切换面时的速度很小。单纯的指数趋近，运动点逼近切换面是一个渐近的过程，不能保证有限时间内到达，切换面上也就不存在滑动模态了，所以要增加一个等速趋近项，使当接近于零时，趋近速度是而不是零，可以保证有限时间到达。

引理：针对，不等式方程，的解为 其中，为任意常数。

  所以采用指数趋近律时，可使系统向趋近，并稳定在其上。此时可获得系统控制律为：

三、Simulink仿真实例

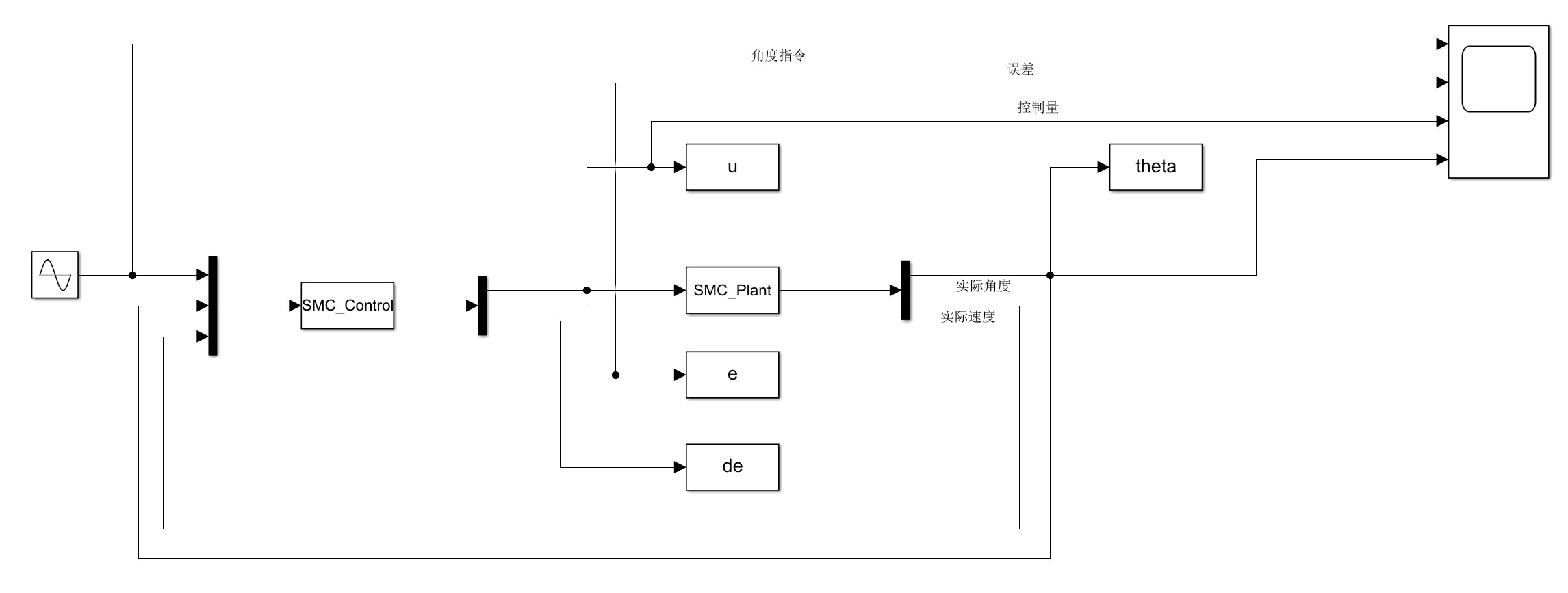
  另考虑二阶系统的滑模控制，有如下控制对象：   其中，。指令信号，频率为，被控对象初始状态为，采用基于指数趋近律的滑模控制律，取，系统的状态空间方程如下（其中取）： Simulink滑模控制结构

SMC_Control文件：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
%{
t: 系统时间
x :系统状态
u: 系统输入，即为Simulink中输入给S-Function的数据
flag: 系统状态，自动生成，返回的flag决定系统当前执行到哪个S-Function子函数
%}
function [sys, x0, str, ts] = SMC_Control(t, x, u, flag)
switch flag
    case 0
        [sys, x0, str, ts] = mdlInitializeSizes;
    case 3
        sys = mdlOutputs(t, x, u);
    case {2, 4, 9}
        sys = [];
    otherwise
        error(['Unhandled flag = ', num2str(flag)]);
end
function [sys, x0, str, ts] = mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;% 连续状态变量数
sizes.NumDiscStates = 0;% 离散状态变量数
sizes.NumOutputs = 3;% 输出变量数
sizes.NumInputs = 3;% 输入变量数
sizes.DirFeedthrough = 1;% 设置输入端口的信号是否在函数mdlOutputs中使用,即其中是否出现u
sizes.NumSampleTimes = 0;
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [];
function sys = mdlOutputs(t, x, u)
thd = u(1); % 输入变量1为角度指令
dthd = cos(t);
ddthd = -sin(t);

th = u(2);  % 输入变量2为实际角度
dth = u(3);% 输入变量3为实际速度

c = 15;
e = thd - th;
de = dthd - dth;
s = c * e + de;

fx = 25 * dth;
b = 133;

epc = 5;
k = 10;
ut = 1 / b * (epc * sign(s) + k * s + c * de + ddthd + fx); % 滑模控制律

sys(1) = ut;    % 输出变量1为控制量
sys(2) = e;     % 输出变量2为误差
sys(3) = de;    % 输出变量3为误差一阶导数

SMC_Plant文件：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
%{
t: 系统时间
x :系统状态
u: 系统输入，即为Simulink中输入给S-Function的数据
flag: 系统状态，自动生成，返回的flag决定系统当前执行到哪个S-Function子函数
%}
function [sys, x0, str, ts] = SMC_Plant(t, x, u, flag)
switch flag
    case 0
        [sys, x0, str, ts] = mdlInitializeSizes;
    case 1
        sys = mdlDerivatives(t, x, u);
    case 3
        sys = mdlOutputs(t, x, u);
    case {2, 4, 9}
        sys = [];
    otherwise
        error(['Unhandled flag = ', num2str(flag)]);
end
function [sys, x0, str, ts] = mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2; % 连续状态变量数
sizes.NumDiscStates = 0; % 离散状态变量数
sizes.NumOutputs = 2; % 输出变量数
sizes.NumInputs = 1; % 输入变量数
sizes.DirFeedthrough = 0;% 设置输入端口的信号是否在函数mdlOutputs中使用,即其中是否出现u
sizes.NumSampleTimes = 0;% 需要的样本时间，一般为1
sys = simsizes(sizes);
x0 = [-0.15, -0.15]; % 状态变量初始值
str = [];
ts = [];
function sys = mdlDerivatives(t, x, u)% 产生系统状态导数
sys(1) = x(2); 
sys(2) = -25 * x(2) + 133 * u;
function sys = mdlOutputs(t, x, u)% 产生系统输出
sys(1) = x(1);  % 输出变量1为角度theta
sys(2) = x(2);  % 输出变量2为速度dtheta

to-workspace模块设置如下所示：

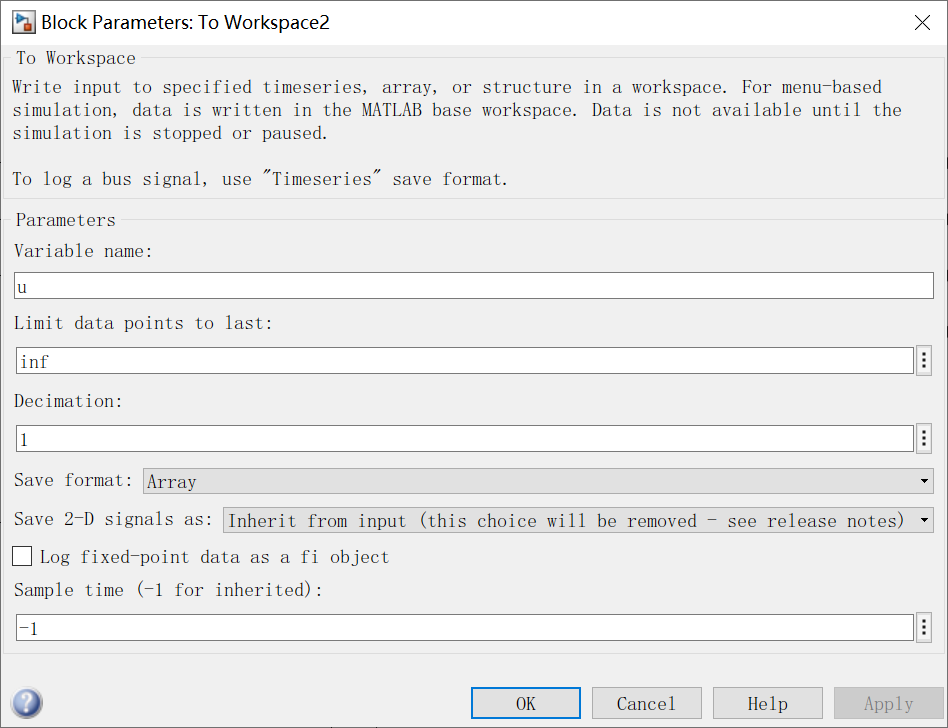
To-workspace模块设置

控制效果如下图所示

滑模控制效果