直流电机DC-Motor位置控制模型

  直流电机是将直流电能转换为机械能的转动装置。电动机定子提供磁场，直流电源向转子的绕组提供电流，换向器使转子电流与磁场产生的转矩保持方向不变。根据是否是否配置有常用的电刷-换向器可以将直流电动机分为两类，包括有刷直流电动机和无刷直流电动机。

参考：

无刷直流电机Vs有刷直流电机

Control Tutorials for MATLAB and Simulink - Motor Position: System Modeling (密歇根大学)

PID控制参数整定（调节方法）-CSDN博客

pid参数作用-CSDN博客

  有刷直流电机中含有电刷进行电流换向，而无刷直流电机中通过电子换向器对电流进行换向，从而产生变化的磁场（一般包含在电机驱动器中）。为对直流电机进行精确的位置控制，需要对其进行控制模型建立，揭示电机转动角位置与输入角指令之间的传递函数模型。

一、直流电机物理模型

  是直流电动机直接提供旋转运动，并与转轴上的负载相结合，可以提供旋转运动。电枢的等效电路和转子的负载受力图如下图所示。

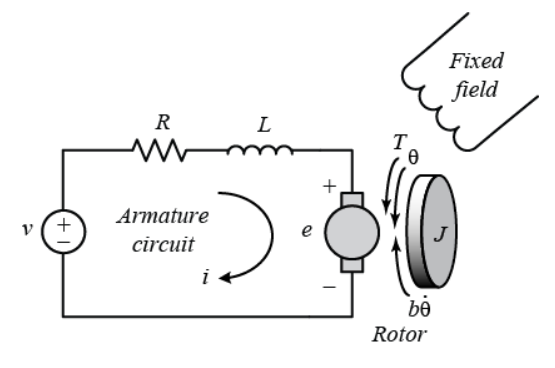
  在上述模型中，我们假设系统的输入是施加在电机电枢上的电压源()，而输出是轴的角位置()。假设转子和轴是刚性的。我们进一步假设一个粘性摩擦模型，即转轴摩擦力矩与轴角速度成正比（根据情况自定义）。为建立直流电机的控制模型，需提供以下参数：

参数	符号	单位
转子的转动惯量（包括转轴上的负载）
电机粘性摩擦常数
反电动势常数
电机转矩常数
电阻
电感

二、直流电机系统方程

  一般来说，直流电机产生的转矩与电枢电流和磁场强度成正比。在这个例子中，我们将假设磁场是恒定的，因此，电机转矩只与电枢电流正比于一个常数因子，如下面的等式所示。这被称为电枢控制的电机。

  对于反电势而言，其值的大小与转轴的速度以一常系数成比例。   转轴的摩擦力矩的大小与转轴的速度以一常系数成比例。   根据牛顿第二定律和基尔霍夫电压定律推导出以下模型方程。

(1)传递函数

  应用拉普拉斯变换，上述模型方程可以用拉普拉斯变量表示。

  通过消除上述两个方程之间的，我们得到以下开环传递函数，当转速被作为输出，电枢电压被作为输入，可得如下方程：

  然而，一般情况，我们将把位置视为输出。我们可以通过对速度积分得到位置，因此，我们只需要将上面的传递函数除以。

(2)状态空间

  通过选取电机位置、电机转速和电枢电流作为状态变量，可以将上述微分方程表示为状态空间形式。同样，电枢电压被视为输入，旋转位置被选择为输出。

(3)系统框图

  在下图中，电气特性传递函数中，在负载特性传递函数中，电机转矩常数，反电势系数。

(4)稳定性分析

  闭环系统稳定性分析方法有多种，例如劳斯判据，Bode图以及Nyquist图。

1. 劳斯判据

  劳斯判据（劳斯–赫尔维茨稳定性判据Routh–Hurwitz stability criterion），又称为代数稳定判据。劳斯于1877年提出的稳定性判据能够判定一个多项式方程中是否存在位于复平面右半部的正根，而不必求解方程。劳斯判据，这是一种代数判据方法。它是根据系统特征方程式来判断特征根在S平面的位置，从而决定系统的稳定性。由于不必求解方程，为系统的稳定性的判断带来了极大的便利。

​ 总结其应用过程可分为两步：

1. 获得闭环系统特征方程，并将其转换成多项式形式

2. 依据特征多项式的各项系数，列取计算劳斯表

• 第一列所有系数为正，则根都在复平面左半平面，系统稳定；
• 第一列有符号变换，变化的次数等于复平面右半平面根的个数，系统不稳定。

计算劳斯表的注意事项：

• Case 1: 某行第一个元素是0，但后面元素不是0。处理方法：用一个很小数代替0，接着往下算。
• Case 2: 某行全是0。处理办法：用上一行的系数构造多项式，对s求导后替代全0行的元素，接着往下算。

2. 伯德图

  频率特性分析(有时也称为频率响应)是利用开环系统函数来分析闭环系统稳定的主要方法，并借助伯德图分析系统稳定性，相比劳斯代数判断更直观。频率响应有乃奎斯特图(极坐标图)和伯德图(对数坐标图)两种方法。两者相比，极坐标图绘制相对简单些，但精度不是很高，所以有时会影响系统闭环稳定性判断的准确性；伯德图绘制相对复杂些，但判断闭环系统稳定性和准确性较高，且判断稳定性原理相对简单。

  伯德图判断系统稳定性仅针对线性定常的最小相位系统（闭环系统的开环传递函数极点和零点的实部都小于或等于零，则称它是最小相位系统），分析其稳定裕度也是有如此限制。

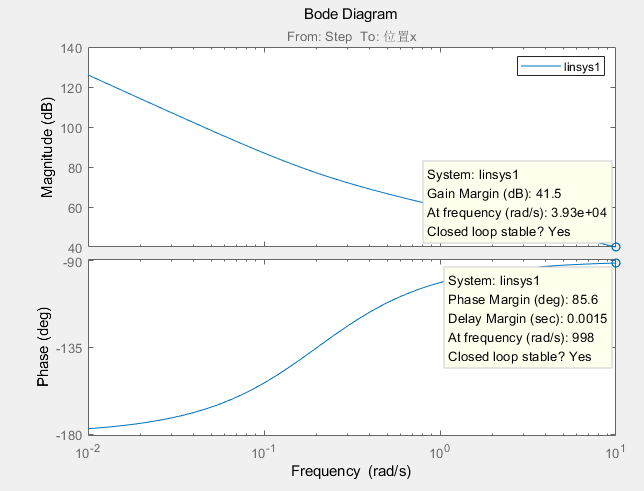
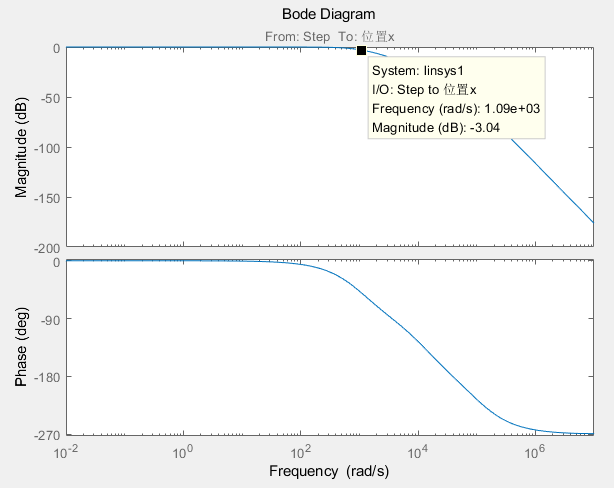
  Matlab中通过在连线中插入Linear Analysis Points的Open-loop Input(Output) 节点，直接绘制系统开环的伯德图，分析其稳定性和稳定裕度；通过在连线中插入Linear Analysis Points的Open-loop Input(Output) 节点，直接绘制系统闭环的伯德图，分析其带宽；

3. 奈奎斯特图

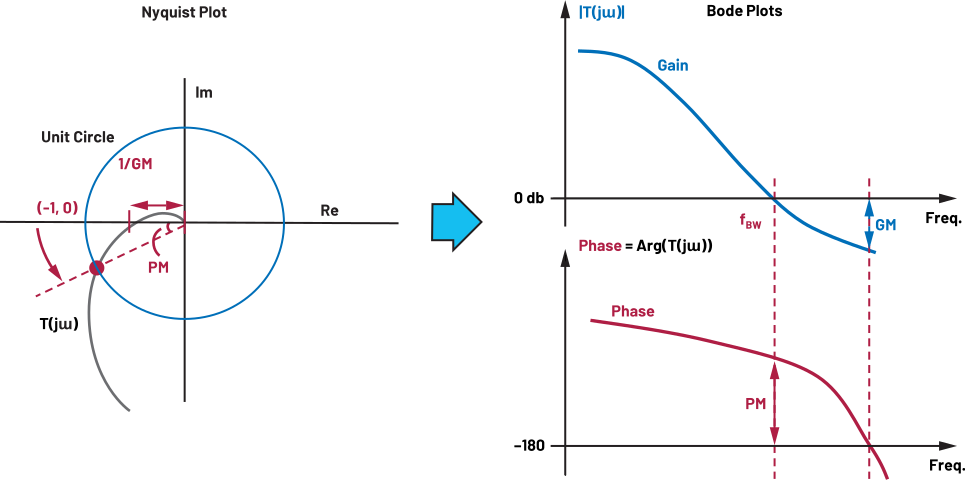
  闭环负反馈系统的稳定性评估可以由开环系统（同一个系统，但不考虑其反馈回路）的奈奎斯特图，配合奈奎斯特稳定判据判断其稳定性。此方法甚至可以用在有延迟的系统，或是非最小相位系统，这些系统用其他方法都很难分析。可以借由图线围绕的次数及开环传递函数右半平面的极点数量来判断稳定性。增益裕度可以用图形越过实轴的数值（幅值裕度），或图线穿过单位圆时的相位（相角裕度）来计算。

!!!注意：频域的稳定裕度判稳方法只对最小相位系统使用，对非最小相位系统进行稳定性判别时应使用奈奎斯特图法，而不是伯德图法。

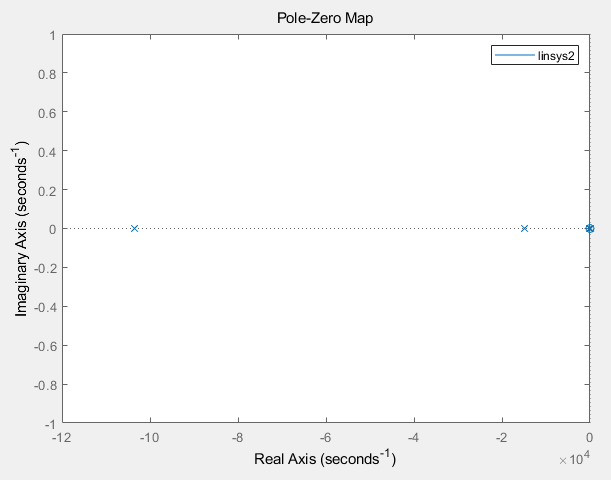
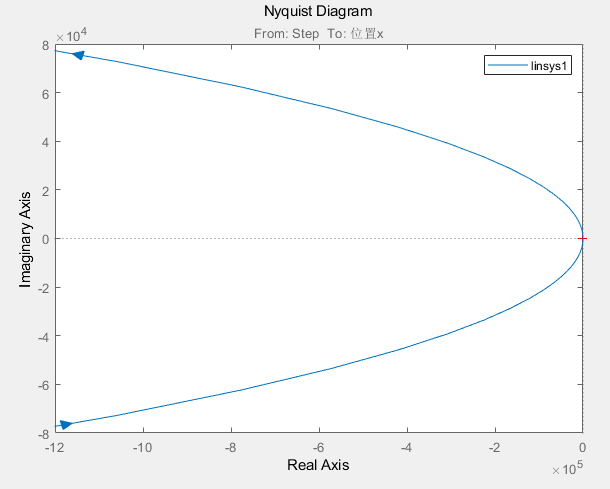
  图中零极点相邻太近区分不开，可以通过右键空白处调整properties选项中的Limits，以查看零极点具体数值，上图中存在5个极点（其中一个极点在原点处），3个零点，通过开环奈奎斯特图绕逆时针旋转圈数是否等于开环右极点数，从上图的奈奎斯特图中看出其不为封闭曲线，为将其封闭需要将其补全，若沿原点右边以无穷大半径的曲线将其封闭，则认为在原点处的极点为左极点。若沿原点左边以无穷大半径的曲线将其封闭，则认为在原点处的极点为右极点，此时该封闭曲线绕逆时针旋转一周刚好等于右极点数。

通过奈奎斯特图可判断任意线性系统的稳定性，但要分析稳定裕度需限制为最小相位系统。

(5)PID参数设置方法

  的基本公式：   的作用概述：

• 比例产生响应速度和力度，过小响应慢，过大会产生振荡，是和的基础。

  是为了建立与目标值和当前值之间误差的一种线性关系，当你的较大的时候，你会很快的到达目标值的附近，但是可能过大，很容易就超过目标值，而超过目标值的时候，你的仍然很大，又会瞬间拉回来，但拉回来的程度会过大，所以也就会出现在目标值附近震荡，没办法收敛于目标值的情况。

• 积分在有系统误差时消除偏差、提高精度，同时也会增加响应速度，产生过冲，过大会产生振荡。

  其实是对的一个补充作用，但我们不能让不断的累加，必须有一个累加的最大值（积分限幅），因为累加过大，会让积分量太大，有可能出现一个跳变，难以控制。把之前所有的偏差进行累加，并把这个累加的值体现在输出上，这样，如果当前值停在了非目标值处，随着时间累加输出值也就会越来越大，最终当前值也会往目标值处走，减小误差。

• 微分抑制过冲和振荡，过小系统会过冲，过大会减慢响应速度。的另外一个作用是抵抗外界的突发干扰，阻止系统的突变。

  的作用是为了给系统一个阻尼，并且系统变化的越快，这个阻尼也就越大，这就能抵消那么粗暴的效果，让温柔一点，在变化小的时候，给小阻尼。在突然一个大变化的时候，阻尼就会很大， 这也就让系统不会变化过快，从而使得系统从震荡趋于稳定。

  工程经验上的试凑调整法：

1. 首先选择一个合适的并且尽量短的采样时间（控制周期）让系统工作；
2. 其次加入比例环节，调节比例系数，直到系统对阶跃指令的输出出现临界振荡；
3. 若单独的比例环节不能满足设计要求，则此时加入积分环节，调整好的比例系数缩小为原来的0.8(或者0.7自行决定)，然后调节积分系数，使得系统能保持较小的稳态误差和较小的振荡时间，此时可以同时调整比例系数和积分系数，知道得到较为满意的结果；
4. 如若还不是特别满意，可以增加微分环节，从小到大逐渐增加微分系数，同时相应的更改比例系数和积分系数，试凑出合适的参数。