跟踪微分器
本文最后更新于:2023年10月21日 上午
跟踪微分器
跟踪微分器(TD,Tracking-Differentiator)由韩京清研究员在《自抗扰控制技术》中提出,是自抗扰控制(ADRC,Active Disturbance Rejection Controller)的一个重要组成部分。跟踪微分器最常见的用途是安排过渡过程,但它作为一种微分器,同样也可以提取含噪信号的微分、配置系统零点、引入相角超前等。
在开始学习跟踪微分器之前,有必要简要的介绍一下PID算法的主要缺点:
从PID的原理可以看出PID的稳定裕度是不小的,但其动态性能的裕度并不大。也就是说,如果被控对像处于一个动态变化的环境之中时,便需要经常改动PID的增益来达到控制效果;
PID算法的核心是:基于误差反馈来消除误差,但有时这种方式并不是最合理的,在初始状态时,直接取这种误差,往往会使初始控制量太大而出现超调的现象,正是这个原因,导致PID算法控制的系统会有“快速性”与“超调”的矛盾;
在实际应用中,由于实际测量很少有比较合适的微分器,导致大部分的系统使用P控制,从而限制了PID的控制能力;
上述描述中,有两个点比较重要,一个是由于初始误差较大而导致控制量大进而导致的超调问题,另一个是微分信号获取得不准确的问题导致PID中的微分项D没有发挥出应有的作用。而跟踪微分器便是一个解决这两个问题的一个较好的工具。
微分-跟踪器(tracking - differentiator, TD)灰信网
跟踪微分器(Tracking Differentiator,TD)_跟踪微分器原理-CSDN博客
ADRC的理解(含效果视频) - 知乎 (zhihu.com)
非线性跟踪-微分器 仿真应用_非线性跟踪微分器-CSDN博客
自抗扰控制2— 跟踪微分器是怎么设计的 (zhihu.com)
【ADRC】一. 线性跟踪微分器 - 知乎 (zhihu.com)
ADRC学习|TD微分跟踪器(原理解析和Matlab实现)_跟踪微分器原理_David小伟同学的博客-CSDN博客
自抗扰控制ADRC之三种微分跟踪器TD仿真分析 (xjx100.cn)
一、微分跟踪器的作用
工程上信号的微分是难以得到的,所以本文采用微分器实现带有噪声的信号及其微分信号提取,从而实现无需量速度信号的控制。并且将会结合一般惯性控制对象,简单地用PID进行控制,即TD微分器+PID控制。
与PID的缺点相对应,跟踪微分器的作用是提供两个信号:一个是目标点的过渡信号,一个是目标点过渡信号的微分信号。过渡信号的意思可以简单的理解为缓慢的向目标点靠近而不阶跃,不超调。即过渡信号可以理解为惯性环节,不超调,缓慢的向目标点生成一条曲线。
(1)经典微分器
假如我们要提取一个信号的微分,最直接也是最简单的想法便是用差分计算,写成传递函数的形式就是一个纯微分环节
由于在现实中无法获得真正的微分
其中,
当时间常数
(2)经典微分器噪声分析
将经典微分器的传递函数利用后向差分进行离散化,将
离散表示为:
当测量信号
其中
(3)线性跟踪微分器
为了消除或减弱噪声的放大效应,考虑用两个惯性环节相减来近似微分器(亦可以理解为纯微分环节串联一个二阶系统,这比经典微分器中惯性环节的噪声抑制能力要强,高频信号抑制能力更强,见下图),这也是微分跟踪器的雏形,如下二阶形式:
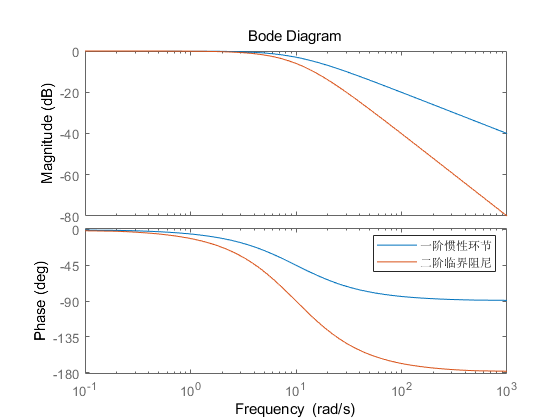
(4)线性跟踪微分器噪声分析
将式后向差分进行离散化,将
离散表示为:% raw %
当测量信号
当两个惯性环节的时间常数一致时:
其中
二、线性跟踪微分器
(1)原理分析
线性跟踪微分器的原理是类似二阶系统的传递函数,如上式
从上式的二阶系统传递函数可知其处于临界阻尼
写成时域方程:
转换成状态空间方程:
即可以理解
(2)仿真验证
1.阶跃信号微分测量
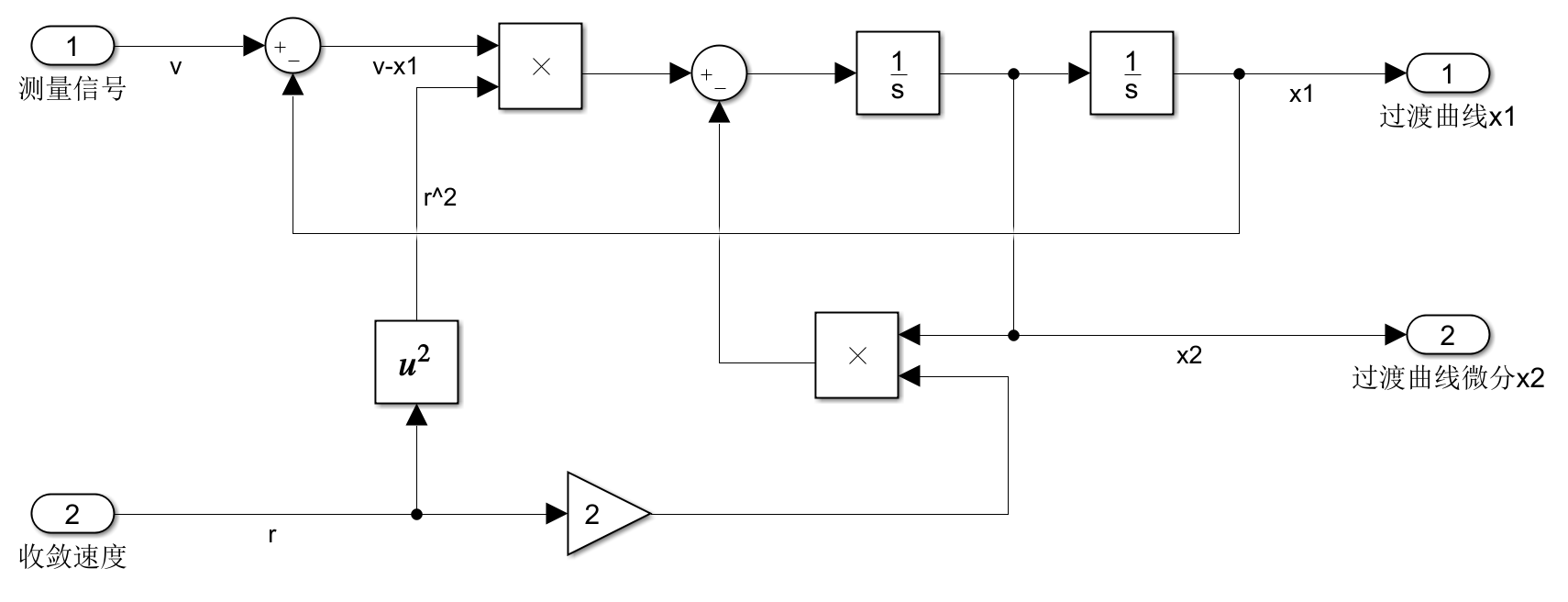
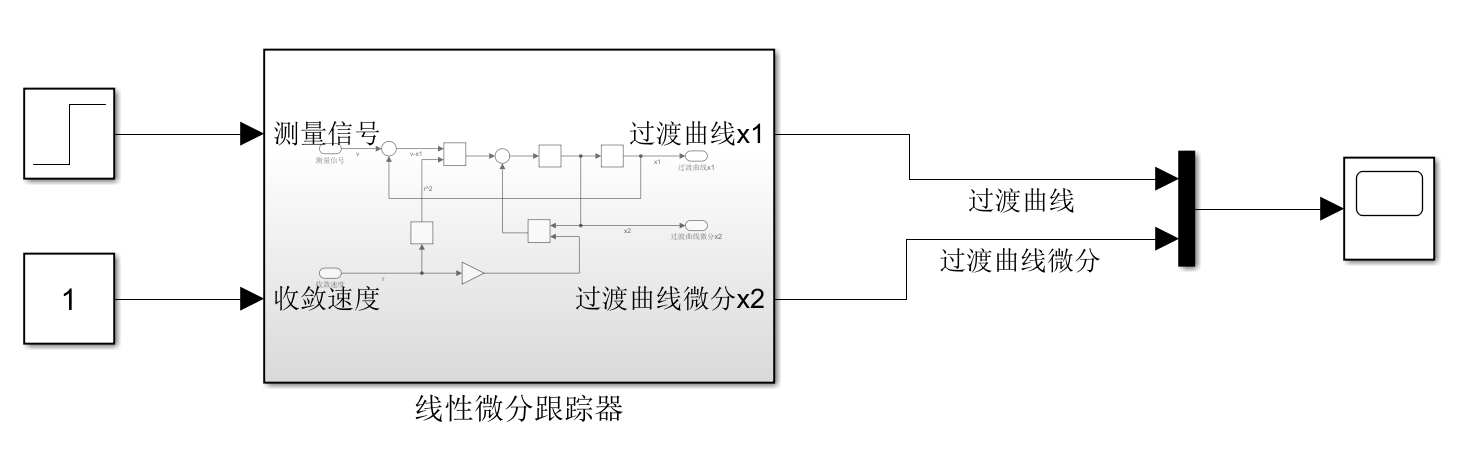
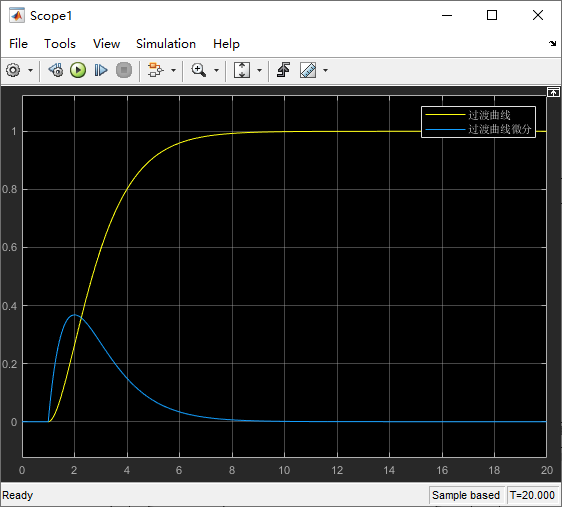
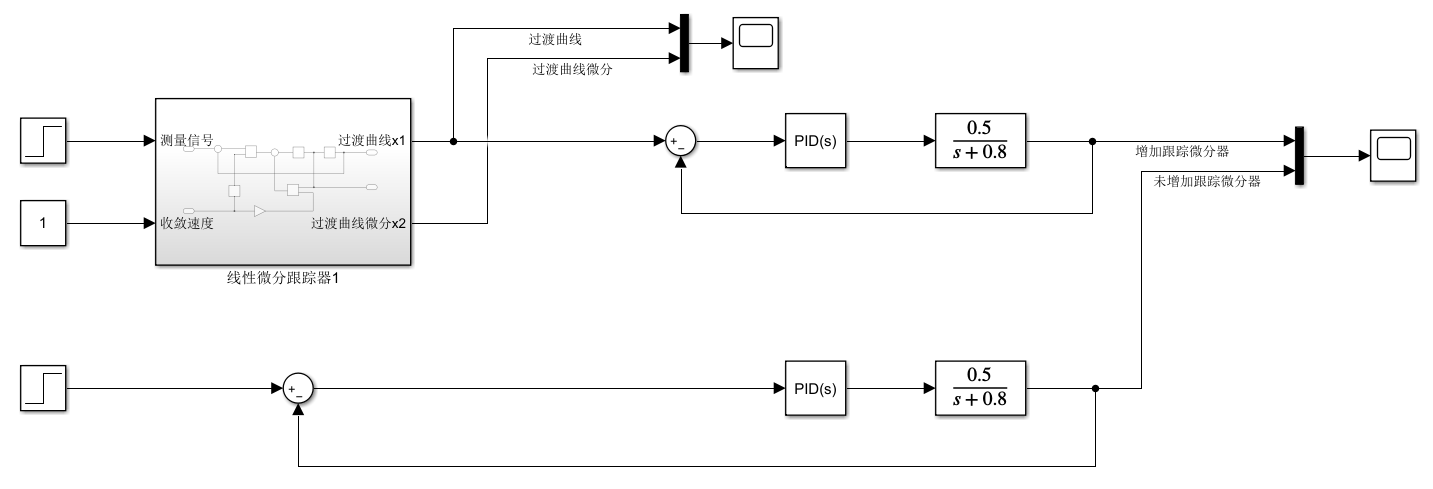
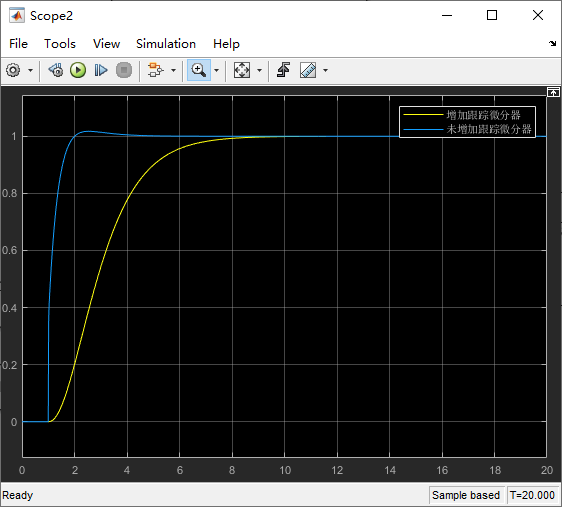
2.优化PID控制
三、非线性跟踪微分器
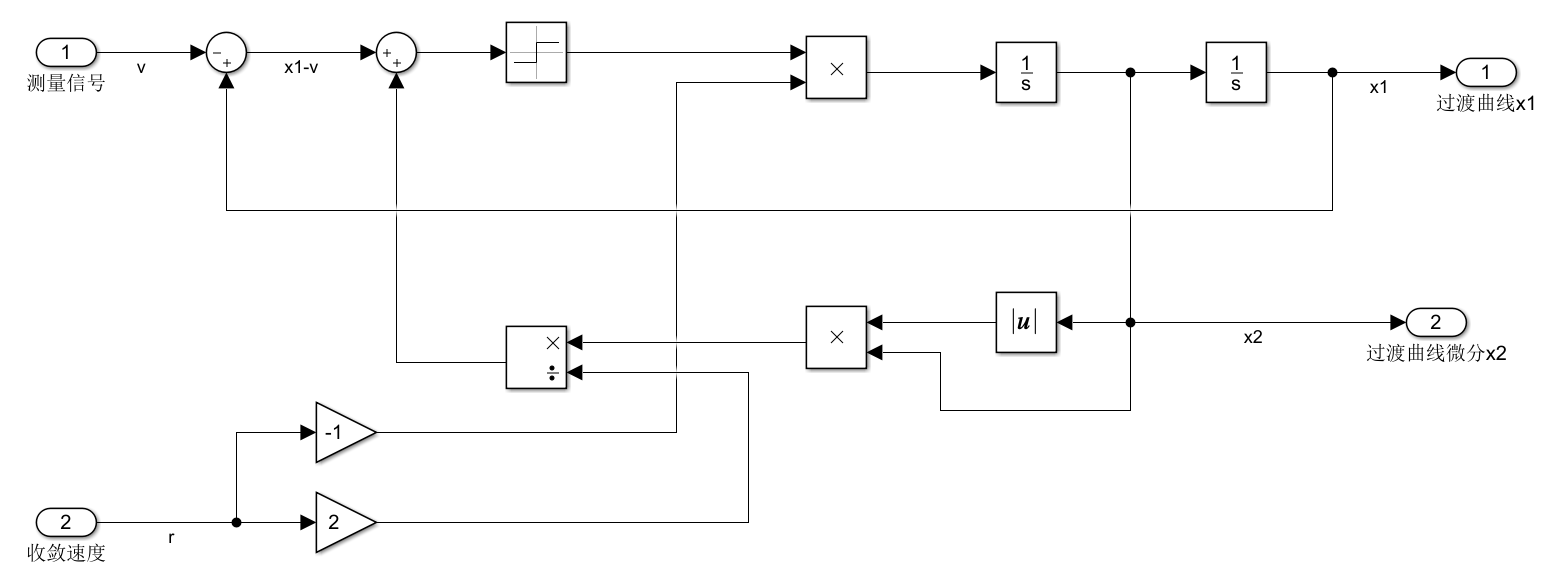
(1)原理分析
非线性跟踪微分器NLTD可以结合线性跟踪微分器LTD进一步分析:其中
对于上式的直观理解,可认为是安排
(2)仿真验证
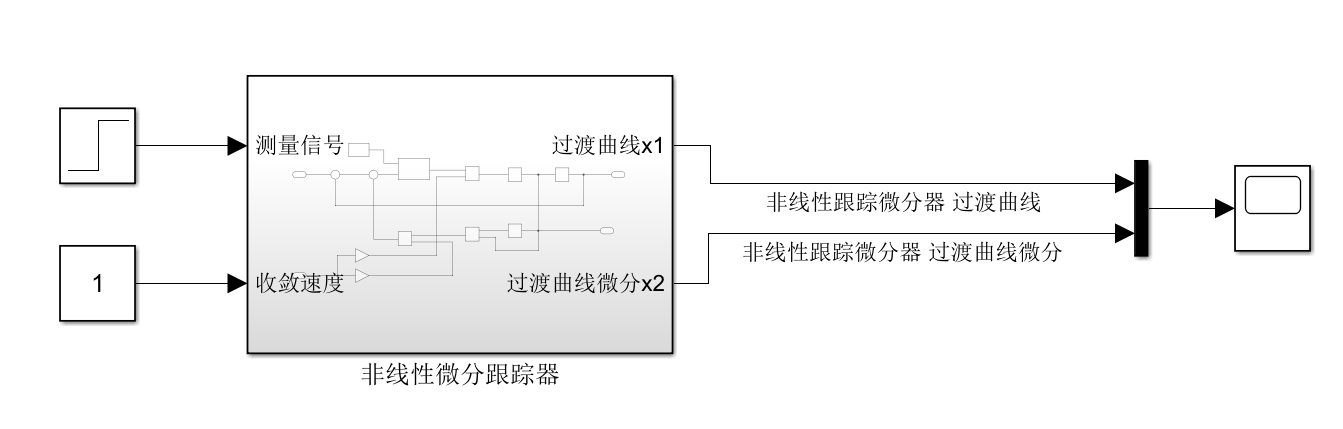
1.阶跃信号微分测量
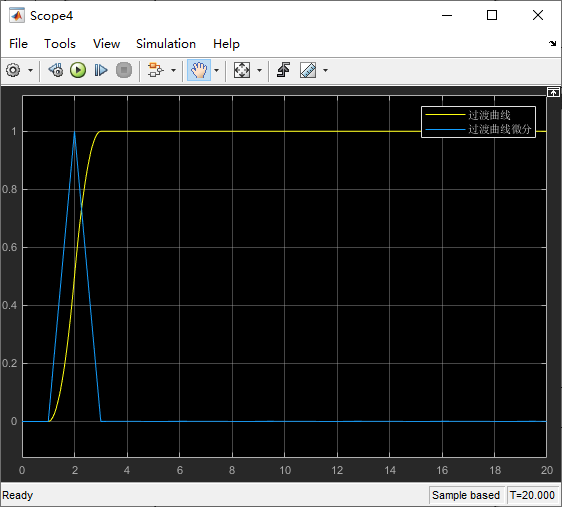
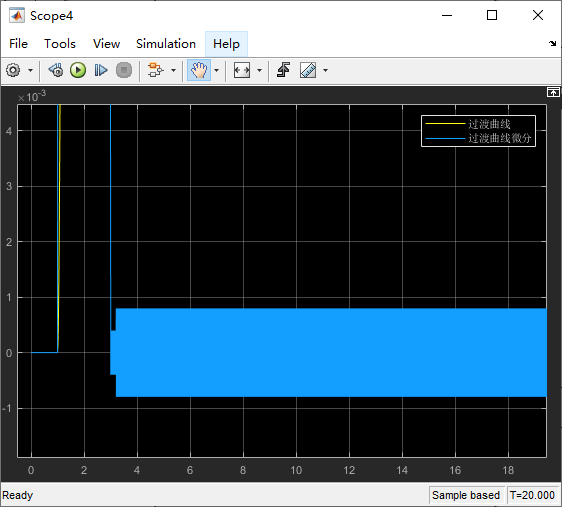
2.颤振改进(改善)
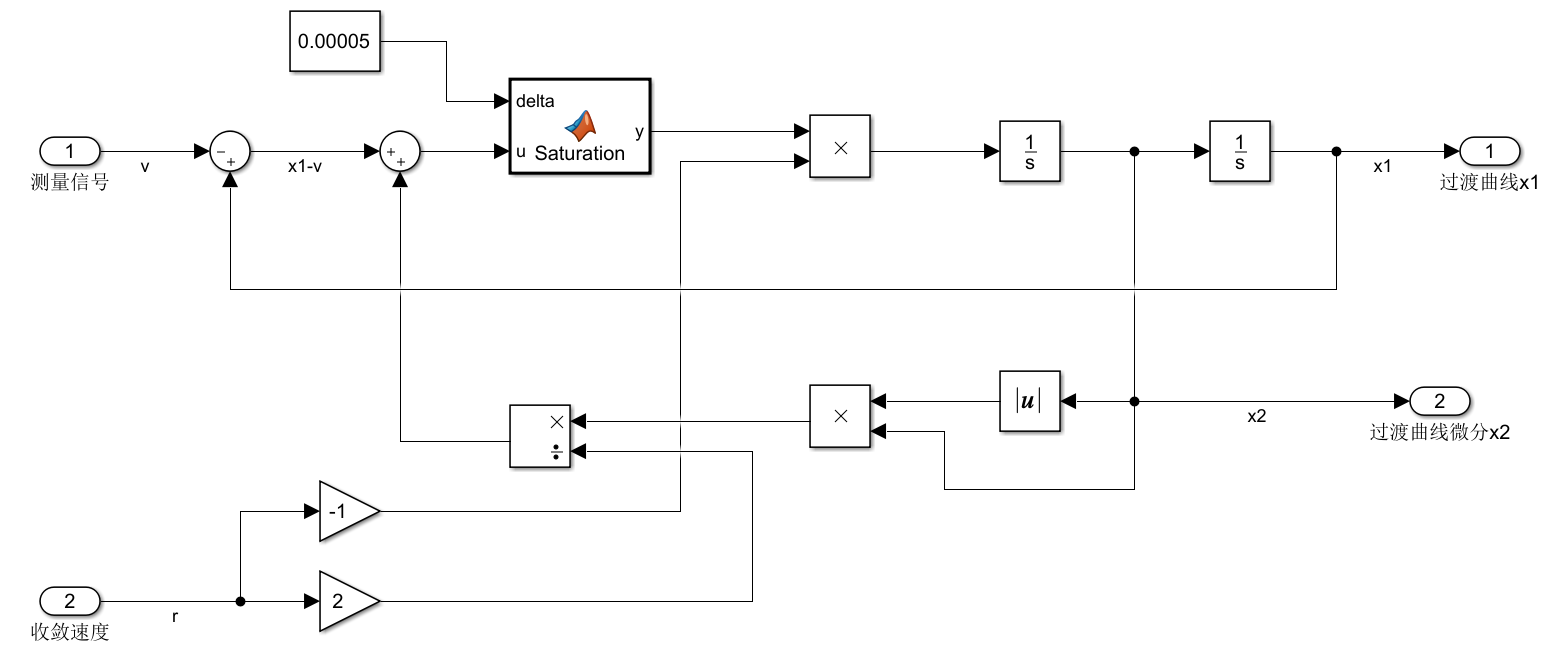
将原来的符号函数替换成线性饱和函数:
1 | |
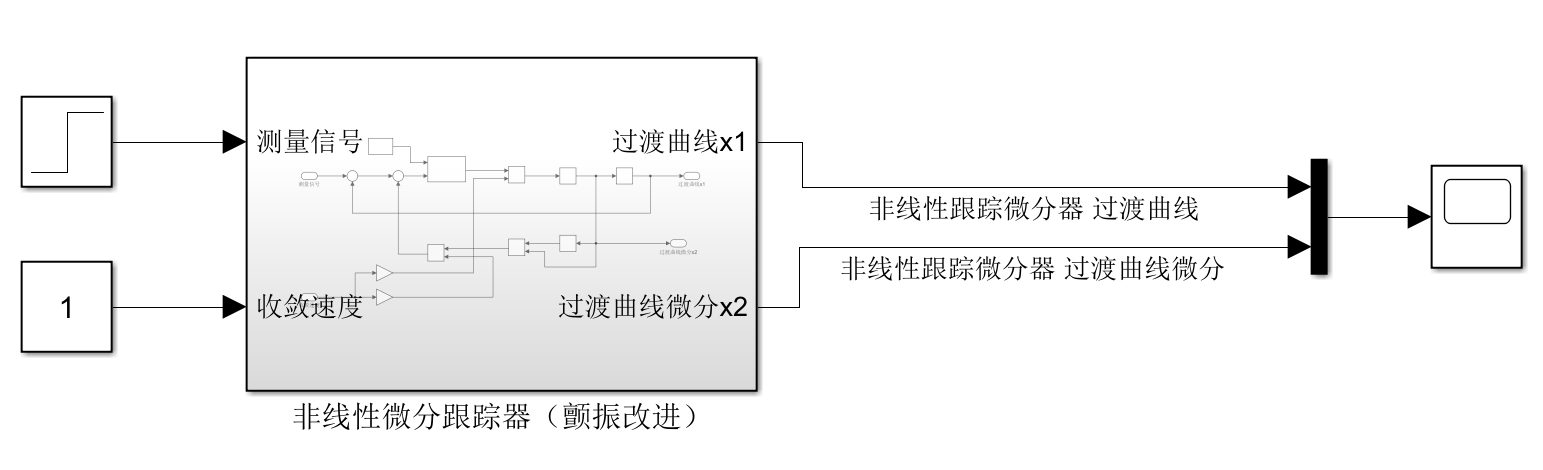
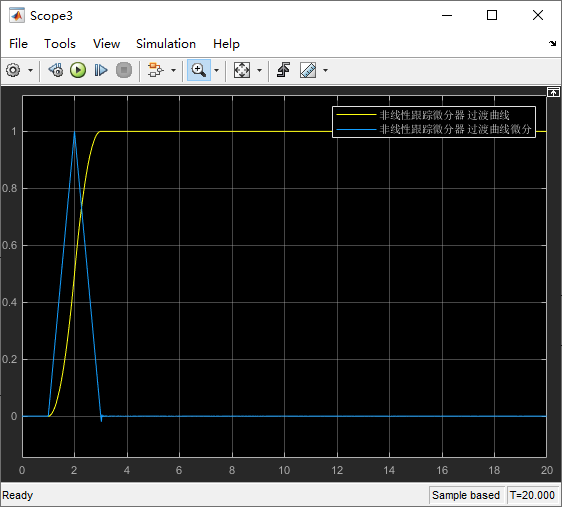
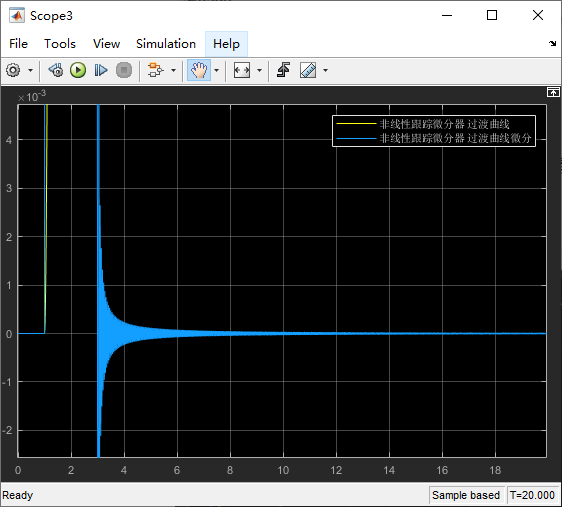
3.优化PID控制对比
针对常规PID控制,引入线性跟踪微分器,对输入信号进行平滑过渡消除纯微分放大噪声的作用,这将会引入信号滞后,通过调试收敛参数

四、最速离散跟踪微分器
(1)原理公式
如果考虑连续系统,上面提到的非线性TD有着非常好的效果,但是我们要处理的实际问题一定是离散的。考虑其离散形式:
这个系统的一个最大问题时,进入稳态后会有高频震颤,将
且最速跟踪微分器的离散表达式为:
(2)仿真验证
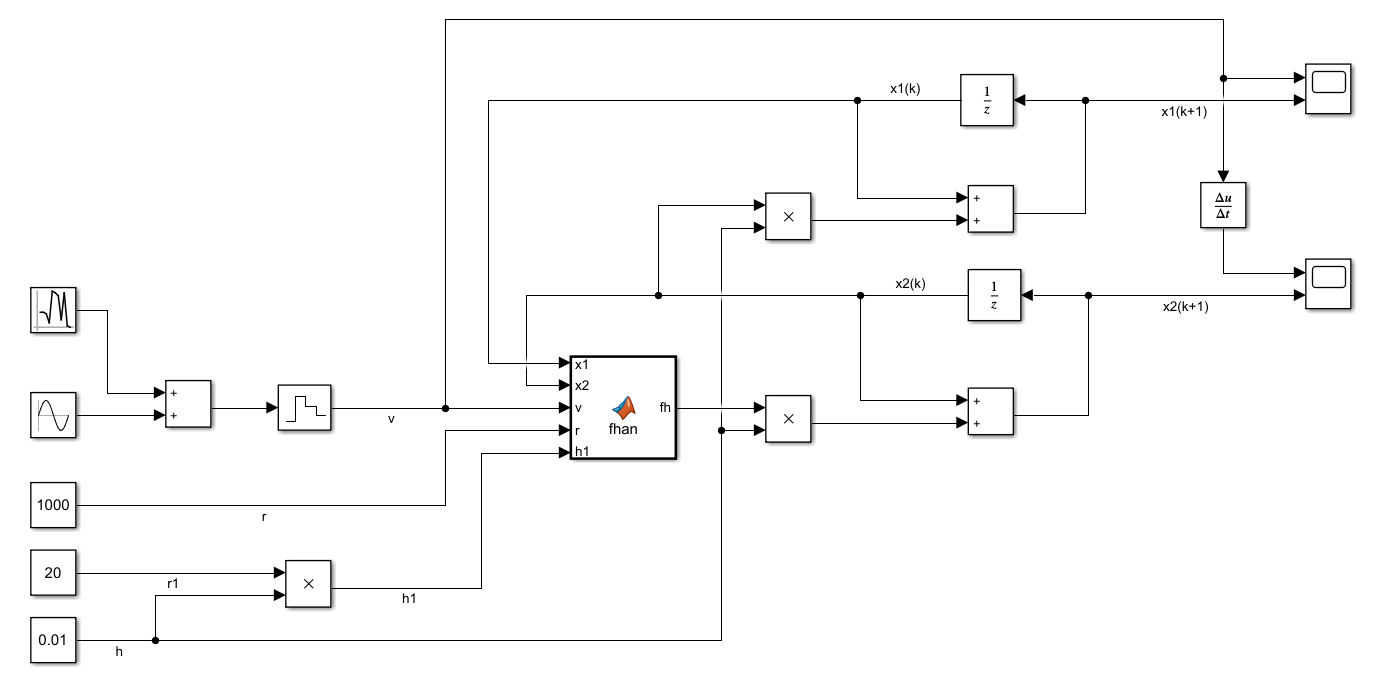
1 | |
Simulink中的仿真步长改为固定步长,且与采样步长
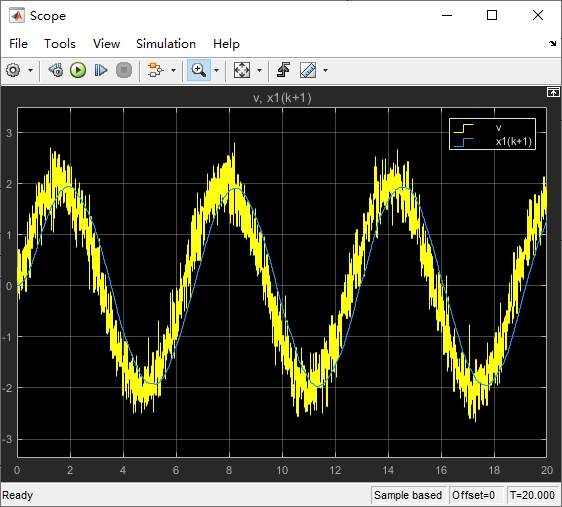
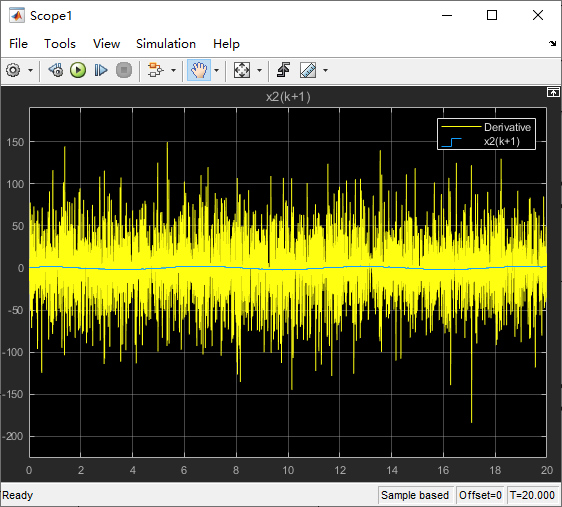
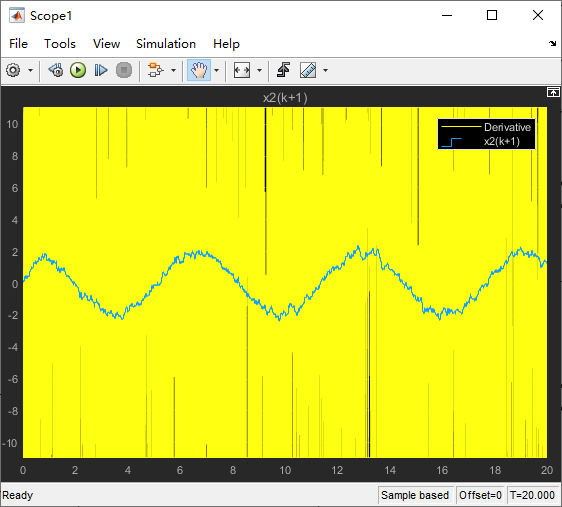
从左图中可以看出跟踪信号存在相位延迟,所以学者武利强在对TD的进一步研究后,由于从TD得到了原始信号的微分,受物理学中位移公式的启发,采用预报的方法来克服延迟。思路是将滤波后得到的信号加上微分信号与预报步长的乘积作为原始信号的逼近,虽然校正了跟踪信号的相位延迟,但是获得的微分信号噪声会变大,读者可查阅该学者文献自行理解。
此节讲述了最速综合控制函数的非线性跟踪微分器,但也有其他非线性跟踪微分器,如全程快速微分器、Levant微分器。理解最速非线性跟踪微分器是学习自抗扰控制的基础,此篇文章作为自抗扰控制的入门篇,后续将更新自抗扰控制。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
