Kalman滤波算法介绍

  卡尔曼滤波在统计学和控制理论中，也被称为线性二次估计(LQE)算法，它使用随时间推移观察到的一系列测量，包括统计噪声和其他不准确性，并通过估计每个时间段上变量的联合概率分布，产生对未知变量的估计，往往比仅基于单一测量的估计更准确。该过滤器以Rudolf E. Kálmán的名字命名，他是该理论的主要开发者之一。

  总的来说，卡尔曼滤波是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。Kalman filter的应用十分广泛，提供了可以真正实用的针对有限维随机系统的实时状态最优估计。它作为一种工具，主要有两方面的应用：状态估计与估计系统的性能分析。

参考文章

如何通俗并尽可能详细地解释卡尔曼滤波？ - 知乎 (zhihu.com)

Kalman Filter Tutorial

附件-Engineering Math常见的物理微分方程 | ShareTechnote

Kalman Filter 卡尔曼滤波 · Sika

图解卡尔曼滤波器如何工作【中文】

图解卡尔曼滤波器如何工作【英文】

Kalman Filter_古路的博客-CSDN博客

协方差矩阵的几何解释

通过简单的推导理解Kalman滤波算法

协方差矩阵最小化 - 知乎 (zhihu.com)

简单易懂-40行MATLAB代码实现卡尔曼滤波 - 知乎 (zhihu.com)

【卡尔曼滤波器】3_卡尔曼增益超详细数学推导 ～全网最完整_哔哩哔哩_bilibili

一、Kalman滤波器

  Kalman Filter算法，是一种递推预测滤波算法，算法中涉及到滤波，也涉及到对下一时刻数据的预测。Kalman Filter由一系列递归数学公式描述。它提供了一种高效可计算的方法来估计过程的状态，并使估计均方误差最小。卡尔曼滤波器应用广泛且功能强大：它可以估计信号的过去和当前状态，甚至能估计将来的状态，即使并不知道模型的确切性质。

  Kalman Filter 也可以被认为是一种数据融合算法（Data fusion algorithm），已有50多年的历史，是当今使用最重要和最常见的数据融合算法之一。Kalman Filter 的巨大成功归功于其小的计算需求，优雅的递归属性以及作为具有高斯误差统计的一维线性系统的最优估计器的状态。

  Kalman Filter只能减小均值为0的测量噪声带来的影响。只要噪声期望为0，那么不管方差多大，只要迭代次数足够多，那效果都很好。反之，噪声期望不为0，那么估计值就还是与实际值有偏差。

(1)假设条件

  理论上，使用kalman滤波器需要满足三个重要假设：

• 系统的动力学模型和测量模型都必须为线性。
• 动力学模型是比较准确的，符合实际系统的行为。
• 动力学模型中的噪音和观测噪音都是零均值且方差已知的白噪声。

(2)递推原理

  当测量一水管的外径时，若我们采用尺子进行多次测量，然后取其平均值作为对此水管外径的精确估计，其过程可描述为：

  多次测量结果、、、…、，求平均值作为估计值：

当前估计值=上一次估计值+系数*(当前测量值-上一次估计值)

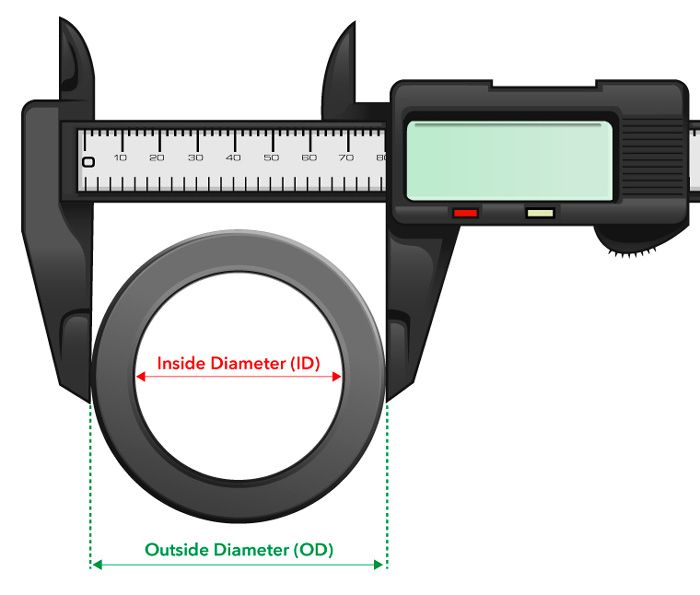
  当测量次数逐渐增加，当前的测量结果越来越不重要了，而当测量次数不够大时，当前测量结果起到作用。

我们引入两个误差，一是估计误差，二是测量误差，将系数由如下表示（后续将详述如何推导）： 讨论：在时刻

若，上一时刻的估计误差远大于当前时刻的测量误差，则，所以更相信当前时刻的测量值；

若，上一时刻的估计误差远小于当前时刻的测量误差，则，所以更相信上一时刻的估计值；

总结上述过程，针对一维数据应用Kalman滤波的步骤为：

Step1：计算Kalman增益；

Step2：计算当前估计值；

Step3：更新当前估计误差；（后续给出推导）

  假如水管外径真实值为，测量误差为（表现测量精度），给出个表格阐述计算过程：

预先给定初始估计值 和估计误差，这两个值可以设定得夸张一些，但是每一次的测量结果肯定是在真实值附近。

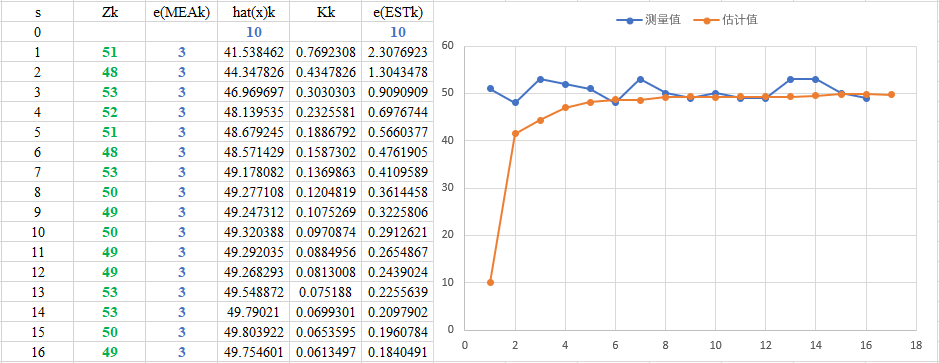
  上述就是利用Kalman滤波的递归思想实现估计值越来越接近真实值的例子。

(3)数据融合

  仍以测量水管外径为例，当存在两把尺子去测量水管外径，两把尺子的测量出来效果有所不同，第一把尺子的测量结果为，方差为，第二把尺子的测量结果为，方差为，如何利用这两把尺子的测量数据来估计真实值是卡尔曼滤波的目的，如果按照主观判断可以推断出真实值可能位于与之间，并且由于第一把尺子的方差小于第二把尺子，所以真实值要靠近第一把尺子的测量结果。

  若利用滤波的思想去描述估计真实值，可表述为如下式子： 当时，估计值将以测量结果1为主；

当时，估计值将以测量结果2为主；

  而现在为求的值使得最小，即使得估计值的方差最小，可推导出的取值公式：

  这样我们就可以求得，那么得到根据两把尺子的测量结果得到的估计值为，同时可求得估计值的方差，其标准差。

(2)应用举例

  以质量-弹簧-阻尼系统为例：

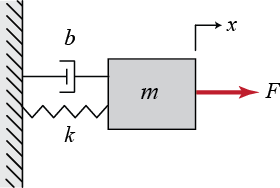
  可列出其动力学方程：

  将作为输入控制量，用进行代替，并取如下状态变量：

  由上获得了质量-弹簧-阻尼系统的动力学方程，再此取测量位置和测量速度作为测量量：   将动力学模型以及测量模型整理成矩阵形式：

  动力学模型：

  测量模型：

  以上的动力学模型方程和测量模型方程的离散形式（状态空间方程的离散化 - 知乎 (zhihu.com)）为：(其中下标表示时间采样的标记)

  在实际生活中任何系统和测量工具都存在有不确定性，当我们考虑这种不确定性时，上式的两个方程则需要改写为：

  其中代表的是过程噪声，而代表的是测量噪声，分别描述的是动力学模型和测量模型的不确定程度。在此我们有了依据动力学模型计算的计算结果以及通过测量得到的测量结果，如何通过这两个数据来源来估计系统的真实值是卡尔曼滤波应用的目的。

(3)Kalman增益

以上述的质量-弹簧-阻尼系统为例，考虑动力学模型中的过程噪声和测量模型中的测量噪声，则有：

在自然环境中，过程噪声向量一般可假设为正态分布，期望为矩阵，方差为过程噪声协方差矩阵，由如下式子表示：

以二维状态向量为例计算协方差矩阵：

由，可将上式转化为：

  同样，测量噪声也可被假设为正态分布，期望为矩阵，方差为测量噪声协方差矩阵，由如下式子表示：

  考虑实际过程中的实现，重新定义动力学模型方程中的符号，若去掉过程噪声项，余下部分是通过理论无偏差模型计算所得的估计值，并且由于未对其做任何的处理，所以将其称为先验估计，以替换。在实际过程中，上一次的值并不是一个真实值，而是一个估计值，所以改写成。

  另外针对测量模型，若去掉测量噪声项，其中是测量结果的估计值，用代替，那么由上述的符号修改可以得到如下两个式子：

  运用之前所介绍的数据融合思想去推导最终的估计值（后验估计）：

  令（为Kalman增益），则有：

  故要寻求最优的，使得，即估计值更好地趋近于真实值。

  定义后验状态误差：

  最优的使得估计误差的分布集中于，也就是使得估计误差的方差最小，而多维状态向量的方差由协方差表示，并且协方差的大小由其迹来衡量。真实值与最优估计值之间误差的协方差可由下式表示：

  将式中的和上述式中的代入求得：

  其中可以定义为先验状态误差，所以式中表达式可写做：

进一步展开化简：

分析中间两项，由于、、为常数，所以上式可写做：

因为先验状态误差和测量噪声相互独立，且有、，所以中间两项为0得：

定义为真实值与先验估计值之间误差的协方差，为测量噪声协方差，则有：

展开公式得：

为求得最小，即使得其矩阵迹最小，并且因为、是常数矩阵，所以求迹：

互为转置矩阵的矩阵，其迹相等，分析和：

可得，所以：

对卡尔曼增益进行求导并求极值点，在此需要结合如下公式：

则有：

协方差矩阵的转置等于自身，整理可得Kalman增益的表达式：

当测量噪声方差非常大时，，根据前述表达式可知，结果更趋近于先验计算值；

当测量噪声方差非常大时，，根据前述表达式可知，结果更趋近于测量值；

至此获得了卡尔曼滤波中的3条重要公式：

①先验估计

②后验估计

③卡尔曼增益

(4)误差协方差矩阵

  在之前的推导过程中，获得了3个重要公式，考虑实际测量计算过程，卡尔曼增益的计算表达式中还存在有不明确的值：

  其中，将式中的和式中的的计算式代入得：

所以式中的可表示为：

因为与相互独立，且各自期望均为0，所以上式中间两项可消掉得：

先验误差协方差需要用到上一次误差协方差，所以需要更新误差协方差，利用式中的表达式得：

将式的卡尔曼增益表达式代入上式有：

至此获得了卡尔曼滤波中另外2个重要公式：

④先验误差协方差

⑤更新误差协方差

总结Kalman滤波的内容，主要分为两个阶段，五个公式：

• 一是预测阶段，包括先验状态计算和先验误差协方差更新

• 二是校正阶段，包括卡尔曼增益更新、估计值计算以及估计误差协方差更新：

由上可以看出，Kalman滤波递推的前提是给定初值和，然后利用常数矩阵的、、以及按照上述、、、、的五个式子进行递推。

整理上述推导过程中所用符号及其含义：

变量	描述	维度
	状态向量
	输出向量
	状态转移矩阵
	输入变量
	控制矩阵
	估计不确定性
	过程噪声不确定性
	测量噪声不确定性
	过程噪声向量
	测量噪声向量
	观测矩阵
	卡尔曼增益
k	离散时间步

维度说明：

• is a number of states in a state vector
• is a number of measured states
• is a number of elements of the input variable

(5)Matlab代码实现

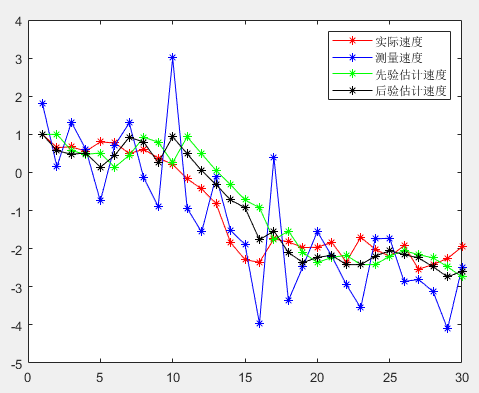
将卡尔曼滤波应用于估计匀速行驶小车的状态为例，取状态1为小车的位置，状态2为小车的速度，则有：

位置转移：

速度转移： 其中为采样时间，表示时刻与时刻的时间间隔。

上述位置和速度转移方程描述的是理想的匀速行驶，而现实过程中会有各种各样的干扰，使得匀速行驶变得不那么匀速行驶，即加上过程噪声项：

可以假设过程噪声符合正态分布，另外利用GPS卫星测量小车的状态，从而建立小车状态的测量模型（理想情况）：

考虑测量的不确定性，将测量模型修正：

所以整理出小车的状态转移方程和观测方程，以矩阵的形式呈现：

即：

根据状态转移方程和观测方程可获得状态转移矩阵和观测矩阵：

根据实际设置过程噪声协方差矩阵和测量噪声协方差矩阵，以确定和，根据卡尔曼滤波的5大公式，利用Matlab实现对匀速行驶小车的状态进行准确估计：

设置采样时间，以及，并给定初始值和。

给出Matlab代码如下：

clear
Q = [0.1, 0; 0, 0.1]; % 过程误差协方差矩阵，Q矩阵
R = [1, 0; 0, 1]; % 测量误差协方差矩阵，R矩阵
A = [1, 1; 0, 1]; % 状态转移矩阵，A矩阵
H = [1, 0; 0, 1]; % 观测矩阵，H矩阵
I = [1, 0; 0, 1]; % 单位矩阵

epoch = 30; % 计算步数（数据量30）
P = [1, 0; 0, 1]; % 估计误差协方差矩阵

X = ones(epoch, 2); % X用来保存实际位置和速度（数据量30）
X(1, :) = [0, 1]; % 实际位置和速度初始化

Xa = ones(epoch, 2); % 后验估计
Xa(1, :) = [0, 1]; % 后验估计值初始化

Xa_ = ones(epoch, 2); % 先验估计
Xa_(1, :) = (A * Xa(1, :)')'; % 先验估计值初始化

Z = ones(epoch, 2); % 测量的位置和速度

for k = 2:epoch
    % 过程误差生成，符合正态分布P(w)～（0，Q）
    w1 = normrnd(0, sqrt(Q(1, 1))); % 位置过程误差
    w2 = normrnd(0, sqrt(Q(2, 2))); % 速度过程误差
    W = [w1, w2];
    X(k, :) = (A * X(k-1, :)' + W')'; % 更新实际位置、实际速度
end

for k = 1:epoch
    % 测量误差生成，符合正态分布P(v)～（0，R）
    v1 = normrnd(0, sqrt(R(1, 1))); % 位置观测误差
    v2 = normrnd(0, sqrt(R(2, 2))); % 速度观测误差
    V = [v1, v2];
    Z(k, :) = (H * X(k, :)' + V')'; %更新测量位置、测量速度
end
for k = 2:epoch
    %预测
    P_ = A * P * A' + Q;
    Xa_(k, :) = (A * Xa(k-1, :)')'; % 先验
    %校正
    K = P_ * H' * inv((H * P_)*H'+R);
    P = (I - K * H) * P_;
    Xa(k, :) = (Xa_(k, :)' + K * (Z(k, :)' - H * Xa_(k, :)'))';
end
plot(1:epoch, X(:, 2), 'r*-', 1:epoch, Z(:, 2), '-b*', 1:epoch, Xa_(:, 2), '-g*', 1:epoch, Xa(:, 2), '-k*')
hold on
legend('实际速度', '测量速度', '先验估计速度', '后验估计速度')

Kalman滤波效果：

二、扩展Kalman滤波器

   扩展卡尔曼滤波（Extended Kalman Filter）是卡尔曼滤波的非线性版本，在状态转移方程确定的情况下，扩展卡尔曼滤波已经成为了非线性系统状态估计的实施标准。 扩展卡尔曼滤波处理非线性问题的主要方法是泰勒展开，求非线性函数的雅可比矩阵。非线性问题一般存在于预测和观测过程，分别对这两部分求雅可比矩阵，作为卡尔曼滤波中的预测矩阵和观测矩阵。

未完待续……