对直角坐标系位姿变换及描述的理解

  任一刚性物体在空间中的静止状态需要由位置及姿态唯一确定，位置描述涉及平移变换，而姿态描述涉及旋转变换，如何在空间中准确描述一物体的位姿，需要了解物体的相对于某个确定坐标系的位姿信息，如若知道多个坐标系之间的相对位姿信息，即可获得该物体相对于中间任意坐标系的位姿描述，这也是坐标系转换的前提。

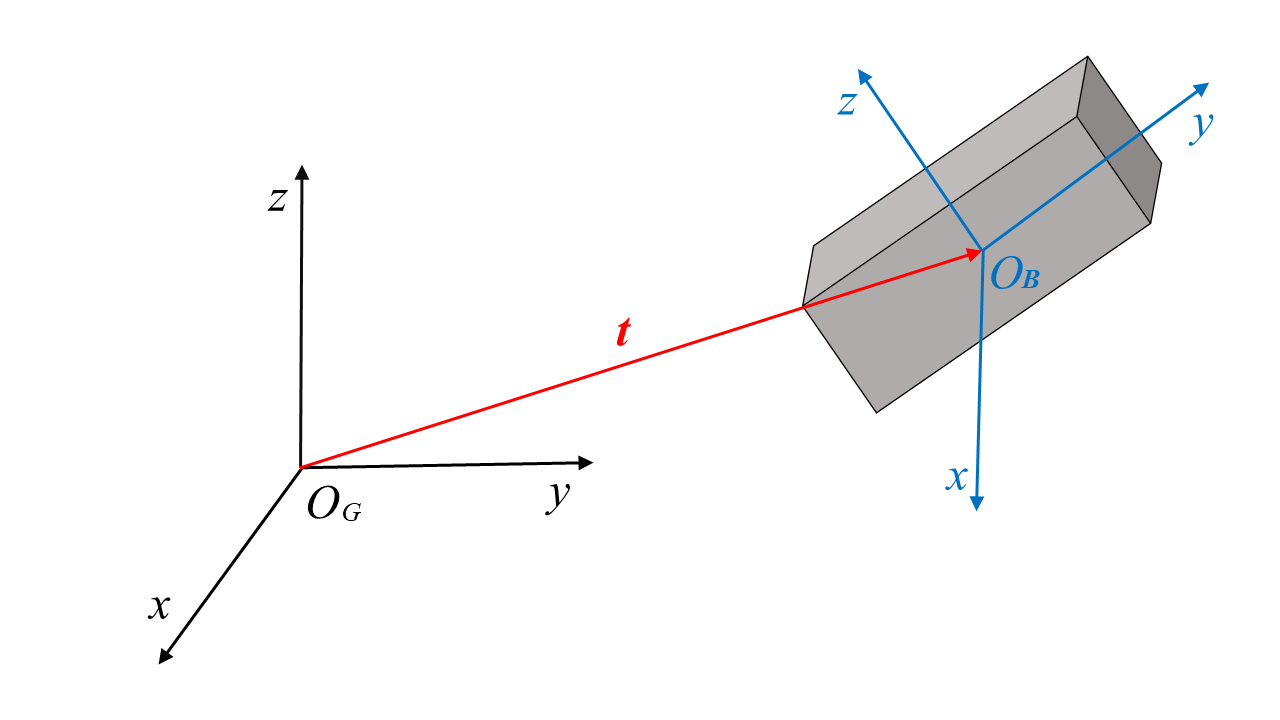
一、空间描述

 (1)位置描述：平移变换

  若仅描述两点之间的相对位置，用向量描述即可。首先需确定参考坐标系，才能确定 XYZ 各轴分量，其矩阵描述如下：

 (2)姿态描述：旋转变换

  要想描述刚性物体在空间中的状态，仅有位置信息时不够的，还需要有姿态信息，即确定与物体固连的坐标系相对与参考坐标系的位姿。通常我们给出旋转矩阵来描述这种相对姿态信息，而这仅仅用于表示两者之间得到相对姿态，并不体现变换过程。

  两坐标系 {A} ， {B} 之间的旋转矩阵 ，所指的就是是 {B} 在 {A} 中的姿态描述：

  ，， 为坐标系 {A} 三坐标轴上的正单位向量；，， 为坐标系 {B} 三坐标轴上的正单位向量。我们可以清晰看出旋转矩阵是由 {B} 各主轴单位向量分别在 {A} 中各主轴的投影（模长均为 1）。

  旋转矩阵具有一些性质例如：旋转矩阵是正交阵，即旋转矩阵的逆等于旋转矩阵的转置

 (3)坐标系描述

  若想完全表示两坐标系的相对状态，需要位置以及姿态信息，所以我们将两者组合用于准确描述两坐标系之间的相对位姿，例如 {B} 在 {A} 中的位姿表示。

  1.混合变换

  如下图，描述坐标系 {C} 在坐标系 {A} 下的位姿

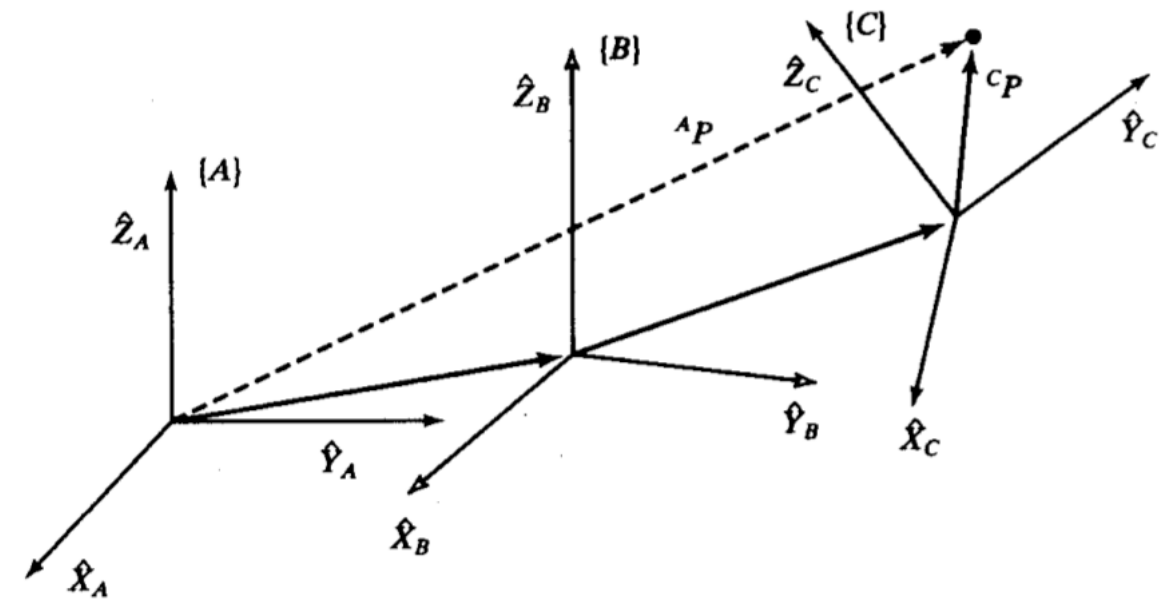
  坐标系 {C} 中的 P 向量 位姿描述转换到坐标系 {A} 中的位姿描述：（ 为 {B} 在 {A} 中的变换描述， 为 {C} 在 {B} 中的变换描述）,列出下列式子：

  求得坐标系{C}中的向量转换到坐标系{A}中的表示，

  2.逆变换

  若已知 {B} 相对于 {A} 的变换 ，要求 {A} 相对于 {B} 的变换 ，即求矩阵的逆。直接的办法就是对转换矩阵求逆，也可以利用变换的性质进行推导：

  旋转矩阵：

  平移矩阵：

  变换矩阵：

 (4)姿态的其他描述方法(欧拉角、四元数、旋转向量（或称为轴角）)

  1.欧拉角

  欧拉角的描述如下图所示，表示两个物体间的相对姿态(通过三个角度 、、 描述姿态)，一般以自身坐标进行旋转的角度称为欧拉角，与以固定参考系进行旋转的角度 RPY 角有所不同。

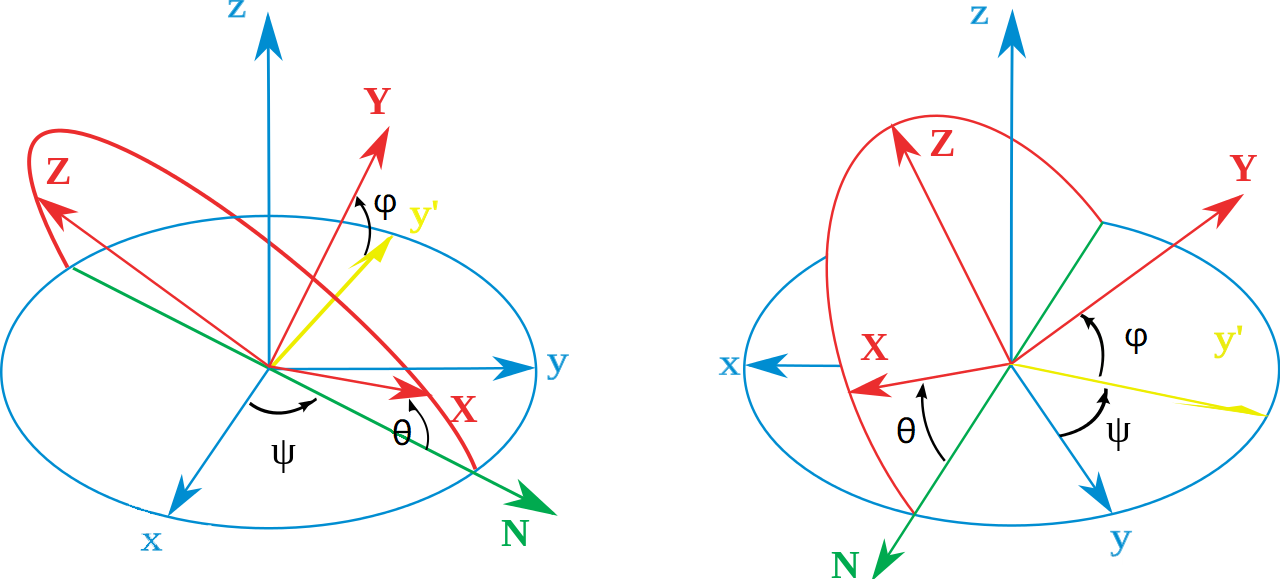
   a.欧拉角的旋转轴和旋转顺序

  表示旋转的欧拉角旋转顺序有 12 种：

  Proper/classic Euler angle：z-x-z，x-y-x，y-z-y，z-y-z, x-z-x，y-x-y

  Tait-Bryan angle（也称作 RPY 角）：x-y-z，y-z-x，z-x-y，x-z-y，z-y-x，y-x-z

  Proper/classic Euler angle 说明这些角度并不是独立的，例如当下面的旋转组合：先绕 x 轴旋转 90 度，再绕 y 轴旋转 90 度，最后绕 x 轴旋转-90 度，这一系列组合得到的效果与只绕 z 轴旋转-90 度是一样的。也就是说我们仅仅在 2 个平面上进行旋转（其中一个平面上必须进行两次旋转）同样可以得到任意的三维旋转！

   b.欧拉角内旋和外旋

  内旋指绕着动坐标系主轴旋转，外旋指绕着静坐标系主轴旋转，内旋右乘，外旋左乘。欧拉角的表述用于确定姿态变换的过程，不同的变换过程确定不同的绕轴旋转顺序以及角度。下列表给出欧拉角的旋转顺序及角度计算

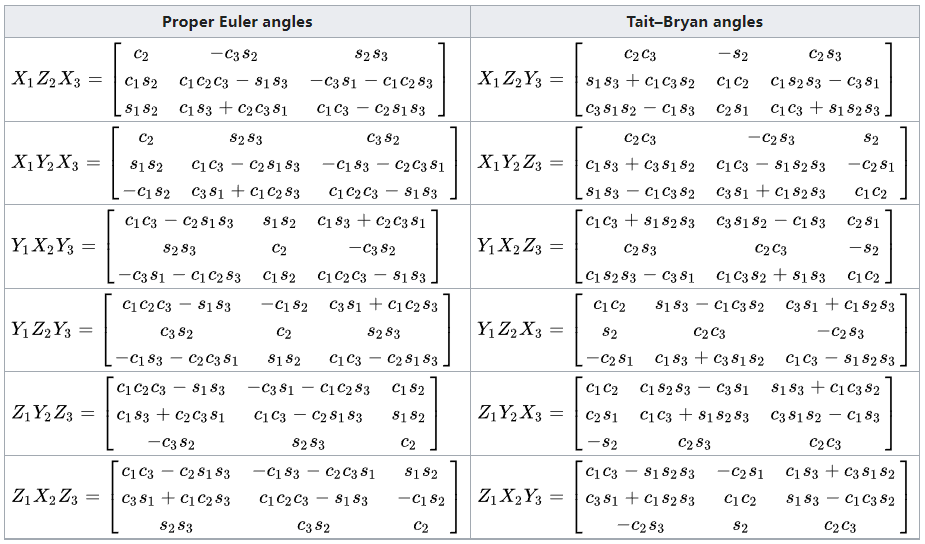
  2.四元数

  一般情况下，两个复数相乘 ，其实就是旋转+伸缩两种变换, 也就是两个复数的模相乘（伸缩）， 辐角相加（旋转），而为了探究三维空间中的旋转变换，爱尔兰数学家哈密顿利用复数发明了四元数，用于描述旋转变换。四元数并不是生来为了解决三维旋转，而是它的性质非常有利于表达旋转信息。四元数相比其他描述形式的优点：

• 解决万向节死锁（Gimbal Lock）问题
• 仅需存储 4 个浮点数，相比矩阵更加轻量
• 四元数无论是求逆、串联等操作，相比矩阵更加高效

   a.四元数组成

  四元数从表达意义上理解和轴角相差无几，也是使用一个 4 个量表示绕此转轴的旋转角度。四元数由 1 个实数和 3 个虚数组成，其表达为 ，其中 ，，，。四元数表达中的 代表旋转轴单位矢量， 代表绕旋转轴旋转的角度大小，并且 ，这便是四元数的常规表达形式

  四元数中的每个数都是经过“处理”的轴和角，轴角描述的四个量并不是一个空间下的东西，首先 是一个 3 维坐标下的矢量，而 则是极坐标下的角度，简单的将他们组合到一起并不能保证他们插值结果的稳定性，因为他们无法归一化，所以不能保证最终插值后得到的矢量长度（经过旋转变换后两点之间的距离）相等，而四元数在是在一个统一的 4 维空间中，方便归一化来插值，又能方便的得到轴、角这样用于 3D 信息数据，所以用四元数再合适不过了。相比于矩阵，四元数也只要存储 4 个浮点数，优势很明显。

   b.四元数使用

  四元数的共轭：

  四元数的模长：

  四元数的逆：

  单位四元数：，逆等于其共轭

  以 为轴，将 旋转 度（右手定则），得到的新向量为

  3.旋转向量

  旋转向量也被称为轴角，其表达 中 代表旋转轴单位矢量（即 ），而 代表绕着旋转轴旋转的角度大小，四元数的组成意义虽和轴角相同，但是其表达形式却不相同。利用轴角进行姿态变换的方法称为轴角法，其具有两个优点也有两个缺点：

  优点 1：同轴的两次旋转可以直接相加来等效为一次旋转；

  优点 2：定义简单，相对直观；

  缺点 1：轴角法表示不唯一，当旋转角度是 0 的时候，旋转轴可以是任意的；

  缺点 2：两次任意的连续旋转无法合成；

 (5)欧拉角、旋转矩阵、四元数、旋转向量之间的转换关系（右手系最常用，教材、OpenCV 以及 Eigen 中都是用右手系，本文也以右手系为准）

  先导知识

  有一些几何变换的推导文章，公式都是正确的，但是很多时候可能会很迷惑，因为他们的公式中的符号可能是相反的。在我们初识三维坐标系时，大都是右手坐标系，但是有些理论是以左手笛卡尔坐标系为基础，所以时常需要进行左手系与右手系的相互转换。

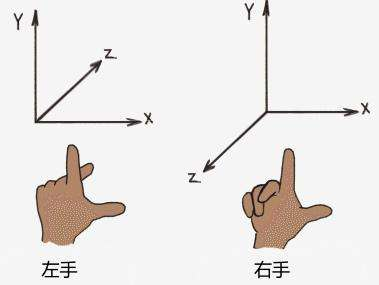
  不管是左手系转右手系还是右手系转左手系，我们都需要这样一个转换矩阵：(此转换矩阵需根据两坐标系之间的轴对应关系确定，在此因两坐标系仅 Z 轴相反，所以转换矩阵如下)

   a.左手系转右手系

  对于向量 ，将其从左手坐标系转换到右手坐标系：

  对于旋转矩阵 ，将其从左手坐标系转换到右手坐标系：

   b.右手系转左手系

  对于向量 ，将其从右手坐标系转换到左手坐标系：

  对于旋转矩阵 ，将其从右手坐标系转换到左手坐标系：

  左手系用左手确定正方向，右手系用右手确定正方向。

  1.欧拉角 ↔︎ 旋转矩阵

   a.欧拉角 → 旋转矩阵

   以右手系下的单轴旋转矩阵获得 顺序欧拉角旋转矩阵

   b.旋转矩阵 → 欧拉角

   利用欧拉角转旋转矩阵求反解：

   观察旋转矩阵各元素特点求解 顺序下各轴旋转角度 ，如下所示，其他旋转顺序的欧拉角可同理求得。

  2.四元数 ↔︎ 旋转矩阵

   a.四元数 → 旋转矩阵

   对于三维坐标的旋转，可以通过四元数乘法直接操作，与旋转矩阵操作可以等价，但是表示方式更加紧凑，计算量也可以小一些。

   若已知四元数

   利用Rodrigues 公式(公式为右手系公式)，将右手系罗德里格公式中的元素按 在前的的格式进行整理后，最终可得右手系下的旋转矩阵：

   其中 ，，，，，，， 为转动角度。

   b.旋转矩阵 → 四元数

   由上式的旋转矩阵 R，利用矩阵中元素可反向计算得出以下 4 组计算式

   那么应该选以上 4 种的哪一种呢？有学者建议首先判断 中哪一个最大，则先计算计算该元素，然后再通过计算方式二中公式计算其他三个分量。因为如果 ，除法就没有意义(分母不能为 0)；如果 非常小，将会出现数值不稳定。为什么这里可以不用考虑开方取正根还是负根的问题？因为此处用到了负四元数的性质，那就是 和 代表相同的旋转。所以只要保证他们的符号是相对一致即可，并且负号并不影响结果。

  3.旋转向量（轴角）↔︎ 旋转矩阵

   a.旋转向量（轴角）→ 旋转矩阵

   假设有旋转向量(轴角) 中，旋转轴单位向量 ，旋转角度为 ，转换后的旋转矩阵为 ，那么 到 的转换其实可以参照四元数转旋转矩阵：

   b.旋转矩阵 → 旋转向量（轴角）

   根据上述旋转矩阵元素排列特点，可得出下述计算式：

   根据矩阵各元素对应相等，可求解 。

  4.欧拉角 ↔︎ 四元数

   a.欧拉角 → 四元数

   欧拉角构造四元数，跟欧拉角构造旋转矩阵一样，就是把三个基础旋转组合在一起，将 欧拉角（或 角：绕固定坐标系的 依次旋转 角）转换为四元数：

   b.四元数 → 欧拉角

   根据上述欧拉角转四元数公式可以求出逆解，即由四元数 到欧拉角 的转换为：

   由于 和 的取值范围在 之间，只有 180°，而绕某个轴旋转时范围是 360°，因此采用计算机计算时要使用 函数代替 函数：

   四元数转欧拉角计算过程中可能会出现旋转自由度丢失的情况，例如俯仰角为 90 度时，会出现 无法计算，所以需要对具体情况进行阈值判断。