粒子滤波算法

  粒子滤波（PF：Particle Filter）的思想基于蒙特卡洛方法（Monte Carlo methods），它是利用粒子集来表示概率，可以用在任何形式的状态空间模型上。其核心思想是通过从后验概率中抽取的随机状态粒子来表达其分布，是一种顺序重要性采样法（Sequential Importance Sampling）。

  简单来说，粒子滤波法是指通过寻找一组在状态空间传播的随机样本对概率密度函数进行近似，以样本均值代替积分运算，从而获得状态最小方差分布的过程。这里的样本即指粒子，当样本数量时可以逼近任何形式的概率密度分布。尽管算法中的慨率分布只是真实分布的一种近似，但由于非参数化的特点，它摆脱了解决非线性滤波问题时随机量必须满足高斯分布的制约，能表达比高斯模型更广泛的分布，也对变量参数的非线性特性有更强的建模能力。因此，粒子滤波能够比较精确地表达基于观测量和控制量的后验概率分布，可以用于解决SLAM问题。

参考

从贝叶斯滤波到粒子滤波 | 朝花夕拾 (shipengx.com)

车辆（十）——粒子滤波 - 知乎 (zhihu.com)

粒子滤波算法理解及实现-CSDN博客

粒子滤波（Particle filter）算法简介及MATLAB实现_粒子滤波算法-CSDN博客

粒子滤波（Particle Filtering）简介_饕子的博客-CSDN博客

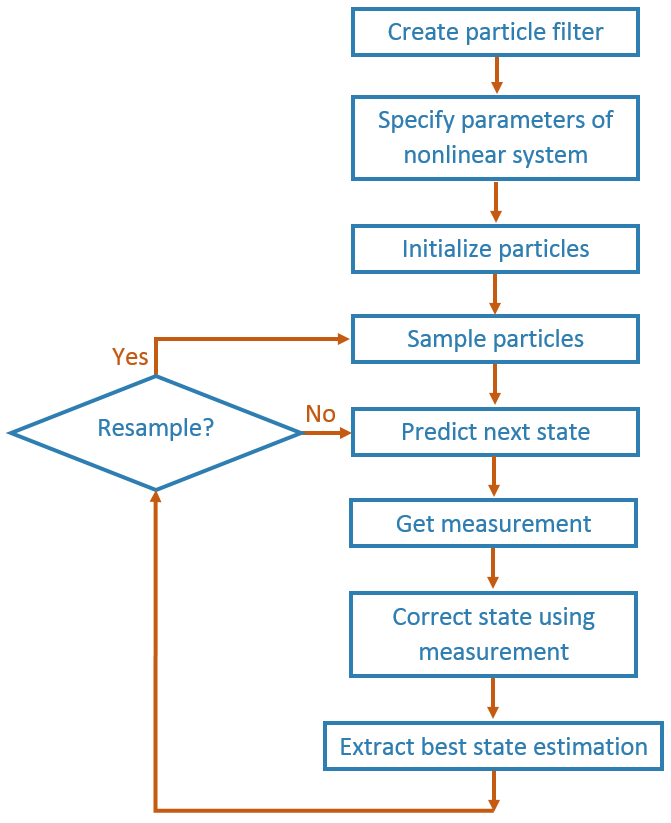
一、算法流程

(1)初始阶段

  在开始滤波过程之前，需要对粒子集合进行初始化。通常可以采用在给定初值处均匀分布或其他分布形式来生成一组粒子，表示系统的初始状态。（本例中采用高斯分布初始化粒子）

(2)预测阶段

  根据系统模型，对每个粒子进行状态转移预测，以得到下一时刻的粒子。

(3)更新阶段

  根据系统模型得到预测值，根据测量结果获得观测数据，以观测值为均值的高斯分布进行每个粒子权重的计算，并进行归一化处理。权重表示了每个粒子与观测数据的一致程度。

(4)重采样阶段

  根据粒子的权重，进行重采样操作（本例中采用独立随机采样，类似轮盘赌），增加高权重的粒子并减少低权重的粒子。重采样操作能够增加高权重粒子的数量，提高估计的准确性，可以通过设置阈值以决定是否进行重采样。

(5)滤波输出

  每一次迭代都会根据系统模型和观测模型，进行状态的预测和更新，从而逐渐减小估计误差。

二、算法思想

(1)均值估计

粒子滤波利用粒子集合的均值来作为滤波器的估计值，前提是粒子集合的分布很好地“覆盖“真实值。

(2)权重计算

根据权重大小能实现”优质“粒子的大量复制，对”劣质“粒子实现淘汰制，是粒子滤波算法的核心。

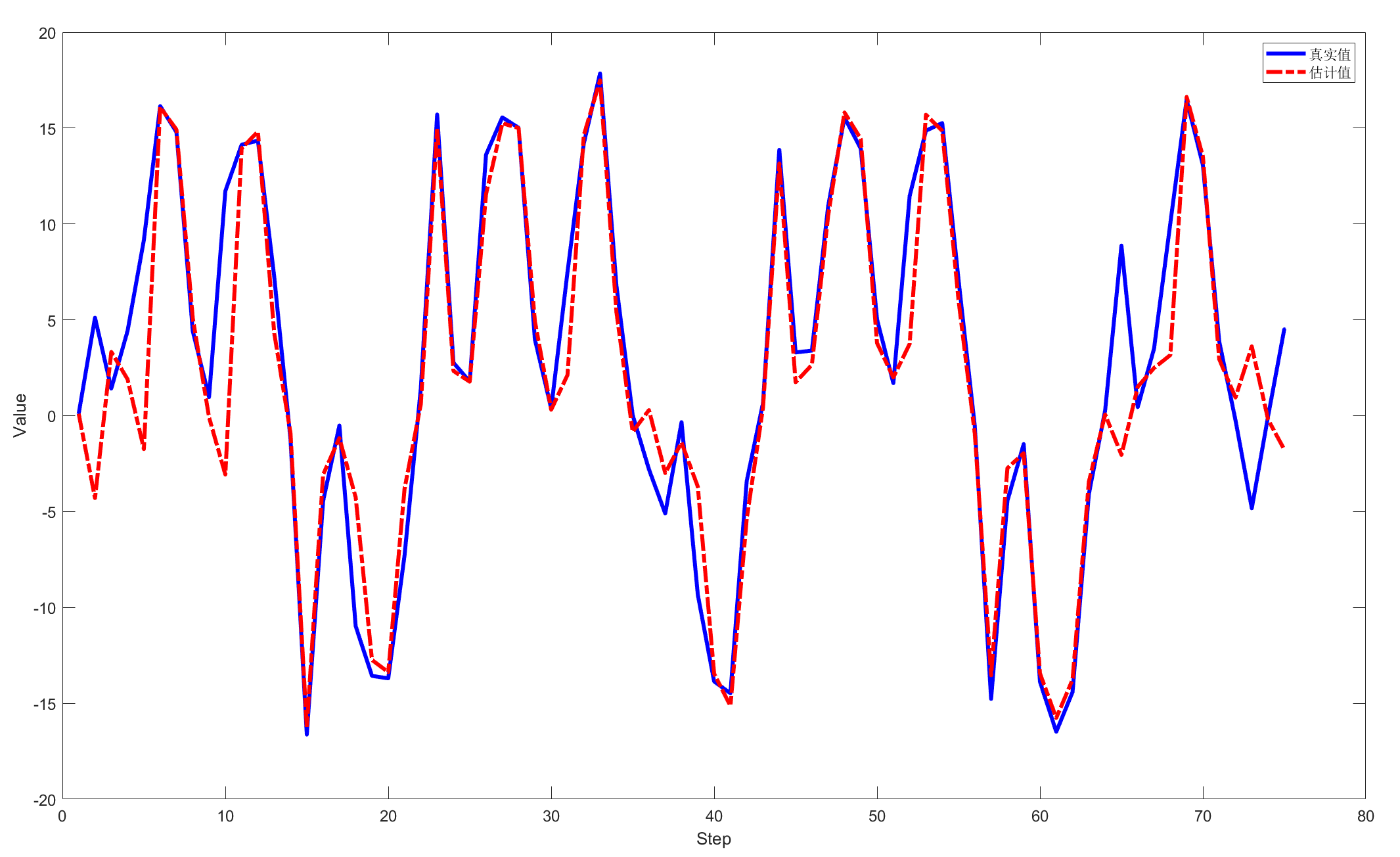
三、代码测试

软件Matlab2018a

% SIR(Sampling Importance Resampling)粒子滤波的应用
clear all
close all
clc

% 初始化
x_init = 0.1; % 初始值
x_N = 1; % 模型噪声的协方差
x_R = 1; % 测量噪声的协方差
T = 75; % 共进行75次
N = 1000; % 粒子数，越大效果越好，计算量也越大

% 将我们的初始先验粒子分布初始化为真实初始值周围的高斯分布

V = 2; % 初始粒子高斯分布的方差
X_ParticleModel = zeros(N, 75); % 沿模型演化获得的粒子值
X_Particle = zeros(N, 75); % 重采样后获得的粒子值
Z_ParticleModel = zeros(N, 75); % 粒子值测量获得的演化序列
Particle_Probility = zeros(N, 75); % 粒子权重演化序列
Particle_NormProbility = zeros(N, T); % 粒子归一化权重演化序列

X_Value = zeros(1, T); % 沿模型演化获得的实际值
X_EstValue = zeros(1, T); % 粒子滤波后的估计值
Z_Value = zeros(1, T); % 实际值对应的测量值

for i = 1:N
    X_ParticleModel(i, 1) = x_init + sqrt(V) * randn(1, 1); % 在初值x=0.1的高斯分布，随机产生初始的N个粒子
end
X_Value(1, 1) = x_init;
X_EstValue(1, 1) = x_init;

for t = 2:T
    % 实际值与观测值在程序中进行虚拟生成，真实环境下实际值无法获取，观测值可以通过测量获得
    % 实际值，系统模型（含高斯不确定量）
    X_Value(1, t) = 0.5 * X_Value(1, t-1) + 25 * X_Value(1, t-1) / (1 + X_Value(1, t-1)^2) + 8 * cos(1.2*(t - 1)) + sqrt(x_N) * randn;
    % 观测值，测量模型，含高斯测量误差
    Z_Value(1, t) = X_Value(1, t)^2 / 20 + sqrt(x_R) * randn;
    for i = 1:N
        % 粒子预测值
        X_ParticleModel(i, t) = 0.5 * X_ParticleModel(i, t-1) + 25 * X_ParticleModel(i, t-1) / (1 + X_ParticleModel(i, t-1)^2) + 8 * cos(1.2*(t - 1)) + sqrt(x_N) * randn;
        % 粒子观测值
        Z_ParticleModel(i, t) = X_ParticleModel(i, t)^2 / 20;
        % 粒子观测值的权重
        Particle_Probility(i, t) = (1 / sqrt(2*pi*x_R)) * exp(-(Z_Value(1, t) - Z_ParticleModel(i, t))^2/(2 * x_R));
    end
    Particle_NormProbility(:, t) = Particle_Probility(:, t) ./ sum(Particle_Probility(:, t)); % 归一化权重
    % 重采样（独立随机采样）
    for i = 1:N
        % 粒子权重大的会有大概率进行保留复制，权重小的粒子数量少
        X_Particle(i, t) = X_ParticleModel(find(rand <= cumsum(Particle_NormProbility(:, t)),1), t);
    end
    
    % 状态估计，重采样以后，每个粒子的权重都变成了1/N，用所有粒子的采样值均值估计真实值
    X_EstValue(1, t) = mean(X_Particle(:, t));
end


t = 1:T;
figure(1);
plot(t, X_Value(1, :), '.-b', t, X_EstValue(1, :), '-.r', 'linewidth', 3);
set(gca, 'FontSize', 12);
set(gcf, 'Color', 'White');
xlabel('Step');
ylabel('Value');
legend('真实值', '估计值');